题目内容
如图，已知△ABC，△CDE都为等边三角形，连接AE，BE，取BE的中点为O，连接AO，并延长AO到F，使BF=AE，求证△BDF为等边三角形．
考点：相似三角形的性质
专题：选作题,立体几何
分析：证明△BCD≌△EFD，可得BD=DF，∠BDC=∠EDF，即可证明△BDF为等边三角形．
解答：
证明：连接EF
∵AO=DF，BO=EO
∴四边形ABFE为平行四边形
即 AB=EF
∵∠FED=180-∠CED=180°-60°=120
又∵∠BCD=∠CDE+∠CED=60°+60=120°
∴∠FED=∠BCD
在△BCD与△EFD中
BC=EF，∠BCD=∠FED，CD=ED
∴△BCD≌△EFD
∴BD=DF，∠BDC=∠EDF
∴∠CDE=∠BDF=60°
∴△BDF为等边三角形．
∵AO=DF，BO=EO
∴四边形ABFE为平行四边形
即 AB=EF
∵∠FED=180-∠CED=180°-60°=120
又∵∠BCD=∠CDE+∠CED=60°+60=120°
∴∠FED=∠BCD
在△BCD与△EFD中
BC=EF，∠BCD=∠FED，CD=ED
∴△BCD≌△EFD
∴BD=DF，∠BDC=∠EDF
∴∠CDE=∠BDF=60°
∴△BDF为等边三角形．
点评：本题考查三角形全等的证明，考查学生分析解决问题的能力，比较基础．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
在斜二侧画法的规则下，下列结论正确的是（ ）
| A、角的水平放置的直观图不一定是角 |
| B、相等的角在直观图中仍然相等 |
| C、相等的线段在直观图中仍然相等 |
| D、若两条线段平行且相等，则在直观图中对应的两条线段仍然平行且相等 |
设x，y∈R，则“x≥2且y≥2”是“x2+y2≥4”的（ ）条件．
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、不充分不必要 |
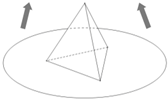某商场为促销要准备一些正三棱锥形状的装饰品，用半径为10cm的圆形包装纸包装．要求如下：正三棱锥的底面中心与包装纸的圆心重合，包装纸不能裁剪，沿底边向上翻折，其边缘恰好达到三棱锥的顶点，如图所示．设正三棱锥的底面边长为xcm，体积为Vcm3．在所有能用这种包装纸包装的正三棱锥装饰品中，V的最大值是多少？并求此时x的值．
已知函数f（x）=Asin（ωx+φ）（其中x∈R，A＞0，ω＞0，0＜φ＜