题目内容
命题p方程:x2+mx+1=0有两个不等的实根,命题q:方程4x2+4(m+2)x+1=0无实根.若“p或q”为真命题,“p且q”为假命题,求m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:先将命题p,q分别化简,然后根据若“p或q”为真命题,“p且q”为假命题,判断出p,q一真一假,分类讨论即可.
解答:
解:由题意命题P:x2+mx+1=0有两个不等的实根,则△=m2-4>0,解得m>2或m<-2,
命题Q:方程4x2+4(m+2)x+1=0无实根,则△<0,解得-3<m<-1,
若“p或q”为真命题,“p且q”为假命题,则p,q一真一假,
(1)当P真q假时:
,
解得m≤-3,或m>2,
(2)当P假q真时:
,
解得-2≤m<-1,
综上所述:m的取值范围为m≤-3,或m>2,或-2≤m<-1.
命题Q:方程4x2+4(m+2)x+1=0无实根,则△<0,解得-3<m<-1,
若“p或q”为真命题,“p且q”为假命题,则p,q一真一假,
(1)当P真q假时:
|
解得m≤-3,或m>2,
(2)当P假q真时:
|
解得-2≤m<-1,
综上所述:m的取值范围为m≤-3,或m>2,或-2≤m<-1.
点评:本题考查命题的真假判断和应用,解题时要认真审题,注意解不等式公式的合理运用

练习册系列答案
相关题目
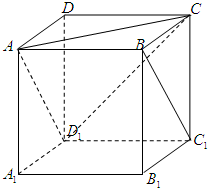 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: