题目内容
已知二次函数y=ax2+bx+c(a>0,c>0,a、b、c为常数)的图象过点(c,0),当0<x<c时,函数值均大于0.若c=2,求a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:由已知中二次函数y=ax2+bx+c(a>0,c>0,a、b、c为常数)的图象过点(2,0),可得b=-1-2a,进而由当0<x<2时,函数值均大于0,可得函数图象的对称轴
=
≥2,进而可得a的取值范围.
| -b |
| 2a |
| 2a+1 |
| 2a |
解答:
解:当c=2时,二次函数y=ax2+bx+c(a>0,c>0,a、b、c为常数)的图象过点(2,0),
即4a+2b+2=0,
即2a+b+1=0,
即b=-1-2a,
又当0<x<c时,函数值均大于0.
即当0<x<2时,f(x)>0.
故二次函数y=ax2+bx+c的图象如下图所示:
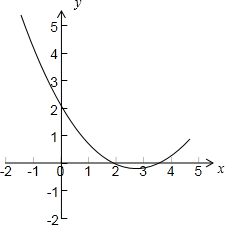
故
=
≥2,
解得:a∈(0,
].
故a的取值范围为:(0,
].
即4a+2b+2=0,
即2a+b+1=0,
即b=-1-2a,
又当0<x<c时,函数值均大于0.
即当0<x<2时,f(x)>0.
故二次函数y=ax2+bx+c的图象如下图所示:

故
| -b |
| 2a |
| 2a+1 |
| 2a |
解得:a∈(0,
| 1 |
| 2 |
故a的取值范围为:(0,
| 1 |
| 2 |
点评:本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
相关题目