Question

2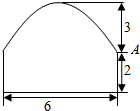．一条隧道横截面由一段抛物线及矩形的三边围成，各段长度见图中所示（单位：米），某卡车空载时可通过此隧道．
（1）现有一集装箱，箱宽3米，装上卡车后箱顶高4.5米，问此车能否通过这条隧道？
（2）若卡车载货板离地面1，4米，为安全起见，装箱顶与隧道顶部距离不少于0.1米，在可以通过随道的情况下，长、宽各为多少米的集装箱截面积最大？

Answer 1

分析 （1）先建立直角坐标系，设出函数关系式，用待定系数法求出函数解析式，因为车从中间过，即x=1.5，代入解析式求出y值后，比较即可；
（2）设刚好通过随道的情况下，长为m、宽为n的集装箱截面积最大．令y=-0.1，代入抛物线方程，解方程可得所求长与宽．

解答 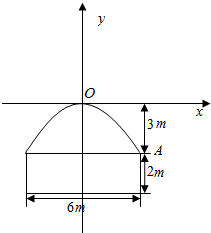解：（1）以隧道横断面抛物线的顶点为原点，
以抛物线的对称轴为y轴，建立直角坐标系，如图，
设抛物线对应的函数关系式y=ax²+bx+c，
因为抛物线的顶点为原点，
所以抛物线过点（0，0），代入得c=0；
隧道宽6m，高5m，矩形的高为2m，
所以抛物线过点（-3，-3）和（3，-3），
代入得-3=9a-3b和-3=9a+3b，
解得a=-$\frac{1}{3}$，b=0．
所以y=-$\frac{1}{3}$x²．
如果此车能通过隧道，集装箱处于对称位置，
将x=1.5代入抛物线方程，得y=-0.75，
此时集装箱角离隧道的底为5-0.75=4.25米，不及车与箱总高4.5米，
即4.25＜4.5．从而此车不能通过此隧道；
（2）设刚好通过随道的情况下，长为m、宽为n的集装箱截面积最大．
令y=-0.1，代入抛物线方程可得x²=0.3，
解得x=$\sqrt{0.3}$
可得当长为5-0.1-1.4=3.5m，宽为2$\sqrt{0.3}$≈1.1m集装箱截面积最大．

点评 本题要建立适当的坐标系，考查了利用待定系数法求抛物线解析式，考查了抛物线的性质和应用，是中档题．