题目内容
12．已知双曲线$\frac{x^2}{4}-\frac{y^2}{m}=1（m＞0）$的离心率为$\sqrt{3}$，则m=8．分析 根据双曲线的标准方程，确定几何量，进而利用离心率公式建立方程，即可求得m的值．
解答 解：∵双曲线$\frac{x^2}{4}-\frac{y^2}{m}=1（m＞0）$，
∴a2=4，b2=m
∴c2=4+m
∵双曲线$\frac{x^2}{4}-\frac{y^2}{m}=1（m＞0）$的离心率为$\sqrt{3}$，
∴${e}^{2}=\frac{{c}^{2}}{{a}^{2}}$=$\frac{4+m}{4}$=3
∴m=8．
故答案为：8．
点评 本题以双曲线的标准方程为载体，考查双曲线的几何性质，确定双曲线的几何量是解题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
已知某几何体的三视图（单位：cm）如图所示，则该几何体表面积是124+2$\sqrt{34}$cm2．
3．将一个各个面上均涂有颜色的正方体锯成n3（n≥3）个同样大小的小正方体，从这些小正方体中任取1个，则其中三面都涂有颜色的概率为（ ）
| A． | $\frac{1}{n^3}$ | B． | $\frac{4}{n^3}$ | C． | $\frac{8}{n^3}$ | D． | $\frac{1}{n^2}$ |
7．已知F1，F2分别为双曲线的左、右焦点，P为双曲线右支上的任意一点，若$\frac{|P{F}_{1}{|}^{2}}{|P{F}_{2}|}$的最小值为8a，则双曲线的离心率e的取值范围是（ ）
| A． | （1，+∞） | B． | （1，2] | C． | （1，$\sqrt{3}$] | D． | （1，3] |
17．已知α∈$（0，\frac{π}{2}）$，β∈$（\frac{π}{2}，π）$，且sinα＞sinβ，则α与β的关系是（ ）
| A． | 0＜β+α＜$\frac{π}{2}$ | B． | $\frac{π}{2}$＜α+β＜π | C． | π＜α+β＜$\frac{3}{2}$π | D． | $\frac{π}{2}$＜α+β＜$\frac{3}{2}$π |
如图，在正方体ABCD-EFGH中，M，N，P，Q，R分别是EH，EF，BC，CD，AD的中点，求证：平面MNA∥平面PQG．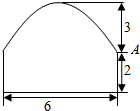
一条隧道横截面由一段抛物线及矩形的三边围成，各段长度见图中所示（单位：米），某卡车空载时可通过此隧道．