题目内容
11．若x，y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{y-x≤2}\\{x≥1}\\{y≥0}\end{array}\right.$，则$\frac{x+y}{x-1}$的最小值为$\frac{4}{3}$．分析 做出不等式表示的平面区域，将$\frac{x+y}{x-1}$化成1+$\frac{y+1}{x-1}$，即求过点（1，-1）的直线斜率的最小值问题．
解答 解：$\frac{x+y}{x-1}$=1+$\frac{y+1}{x-1}$，
做出平面区域如图：
有图可知当过点（1，-1）的直线经过点C（4，0）时，斜率最小为$\frac{1}{3}$，
∴$\frac{x+y}{x-1}$的最小值为1+$\frac{1}{3}$=$\frac{4}{3}$．
故答案为$\frac{4}{3}$．
点评 本题考查了简单的线性规划，是基础题．
练习册系列答案
学习实践园地系列答案
相关题目
如图，在正方体ABCD-EFGH中，M，N，P，Q，R分别是EH，EF，BC，CD，AD的中点，求证：平面MNA∥平面PQG．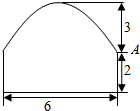
一条隧道横截面由一段抛物线及矩形的三边围成，各段长度见图中所示（单位：米），某卡车空载时可通过此隧道．