题目内容
7．作出正弦型函数y=2sin（3x-$\frac{π}{3}$）在一个周期内的图象．分析 令3x-$\frac{π}{3}$分别等于0，$\frac{π}{2}$，π，$\frac{3π}{2}$，2π，求出x和函数值y，利用五点作图法作出图象．
解答 解：列表
| 3x-$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{9}$ | $\frac{5π}{18}$ | $\frac{4π}{9}$ | $\frac{11π}{18}$ | $\frac{7π}{9}$ |
| 2sin（3x-$\frac{π}{3}$） | 0 | 2 | 0 | -2 | 0 |
点评 本题考查了五点法作三角函数图象，是基础题．
练习册系列答案
相关题目
17．已知α∈$（0，\frac{π}{2}）$，β∈$（\frac{π}{2}，π）$，且sinα＞sinβ，则α与β的关系是（ ）
| A． | 0＜β+α＜$\frac{π}{2}$ | B． | $\frac{π}{2}$＜α+β＜π | C． | π＜α+β＜$\frac{3}{2}$π | D． | $\frac{π}{2}$＜α+β＜$\frac{3}{2}$π |
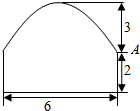一条隧道横截面由一段抛物线及矩形的三边围成，各段长度见图中所示（单位：米），某卡车空载时可通过此隧道．