题目内容
18.己知直线l1:mx-y+2=0(m∈R),直线l2:x+my-2=0,点P是两直线的交点.(1)判断两直线l1、l2的位置关系,并求点P的轨迹C的方程;
(2)已知M(1,1),设Q是直线x+y+2=0上的动点,QA.QB是轨迹C的两条切线,A,B为切点,求四边形QAMB的面积的最小值.
分析 (1)由m×1+(-1)×m=0,可得两直线l1、l2垂直;直线l1:mx-y+2=0(m∈R),直线l2:x+my-2=0联立可得x=$\frac{-2m+2}{{m}^{2}+1}$,y=$\frac{2m+2}{{m}^{2}+1}$,消去参数,可得点P的轨迹C的方程;
(2)由对称性,QM最小时,四边形QAMB的面积最小,此时MQ⊥l2,斜率为1,求出Q的坐标,即可求四边形QAMB的面积的最小值.
解答 解:(1)∵直线l1:mx-y+2=0(m∈R),直线l2:x+my-2=0,
∴m×1+(-1)×m=0,
∴两直线l1、l2垂直,
直线l1:mx-y+2=0(m∈R),直线l2:x+my-2=0联立可得x=$\frac{-2m+2}{{m}^{2}+1}$,y=$\frac{2m+2}{{m}^{2}+1}$,
∴x+y=$\frac{4}{{m}^{2}+1}$,x2+y2=$\frac{8}{{m}^{2}+1}$,
∴2x+2y=x2+y2,
∴点P的轨迹C的方程是(x-1)2+(y-1)2=2;
(2)∵M(1,1)为轨迹C的圆心,
∴由对称性,QM最小时,四边形QAMB的面积最小,此时MQ⊥l2,斜率为1,
由$\left\{\begin{array}{l}{y=x}\\{x+y+2=0}\end{array}\right.$,可得Q(-1,-1),
∴MQ=2$\sqrt{2}$,∴QA=$\sqrt{6}$,
∴四边形QAMB的面积最小值为$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{6}$=2$\sqrt{3}$.
点评 本题考查求四边形QAMB的面积的最小值,考查轨迹方程,考查参数法的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.设函数f(x)=$\left\{\begin{array}{l}{4+x,x≤0}\\{{x}^{2},x>0}\end{array}\right.$,若f[f(a)]>f[f(a)+1],则实数a的取值范围为( )
| A. | (-1,0] | B. | [-1,0] | C. | (-5,-4] | D. | [-5,-4] |
13.一个空间几何体的三视图如图所示,则该几何体的外接球的表面积为( )
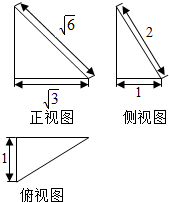

| A. | 5? | B. | 6? | C. | 2$\sqrt{7}$π | D. | 7π? |
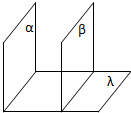 如图,α、β、λ是三个平面,满足α⊥γ,α∥β,求证:β⊥γ.
如图,α、β、λ是三个平面,满足α⊥γ,α∥β,求证:β⊥γ.