题目内容
已知a，b，c，d均为实数，下列命题中正确的是（ ）
| A、a＞b⇒ac2＞bc2 |
| B、a＜b＜0，c＜d＜0⇒ac＜bd |
| C、a＞b，ac＜bc⇒c＞0 |
| D、a＞b，c＞d⇒a+c＞b+d |
考点：不等式的基本性质
专题：不等式
分析：根据不等式的性质判断即可．
解答：
解：对于A，若a＞b，当c=0时，ac2＞bc2不成立，故A错误，
对于B，若a＜b＜0，c＜d＜0，a=-2，b=-1，c=-2，d=-1则ac＜bd不成立，故B错误，
对于C，若a＞b，ac＜bc，则c＜0，故C错误，
对于D，a＞b，c＞d⇒a+c＞b+d，根据不等式的同向可加性，故D正确
故选：D
对于B，若a＜b＜0，c＜d＜0，a=-2，b=-1，c=-2，d=-1则ac＜bd不成立，故B错误，
对于C，若a＞b，ac＜bc，则c＜0，故C错误，
对于D，a＞b，c＞d⇒a+c＞b+d，根据不等式的同向可加性，故D正确
故选：D
点评：本题考查了不等式的基本性质，属于基础题．
练习册系列答案
相关题目
如图，某隧道设计为双向四车道，车道总宽20m，要求通过车辆限高5m，隧道全长2.5km，隧道两侧是与底面垂直的墙，高度为3m，隧道上部拱线近似地看成半个椭圆．（
+
）8的展开式中x2的系数为（ ）
| x |
| 1 | ||
2
|
A、
| ||
B、
| ||
C、
| ||
| D、7 |
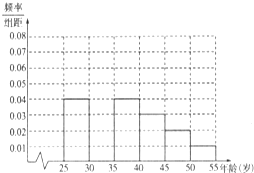某移动公司对[25，55]岁的人群随机抽取n人进行了一次是否愿意使用4G网络的社会 调查，若愿意使用的称为“4G族”，否则称为“非4G族”，得如下统计表和各年龄段人数频率分布直方图：