题目内容
定义在R上的函数f(x)为奇函数且满足f(1+x)=-f(1-x),且x∈(0,1)时,f(x)=2x+
,则f(log25)= .
| 1 |
| 5 |
考点:对数的运算性质,函数奇偶性的性质
专题:函数的性质及应用
分析:由条件可得f(x)=f(x-2),函数f(x)的周期为2,再根据f(log25)=f(log2
),计算求得结果.
| 5 |
| 4 |
解答:
解:由函数f(x)为奇函数且满足f(1+x)=-f(1-x),可得f(1+x)=-f(1-x)=f(x-1),即f(x)=f(x-2),
故函数f(x)的周期为2.
由x∈(0,1)时,f(x)=2x+
,可得f(log25)=f(log25-2)=f(log2
)=2log2
+
=
+
=
,
故答案为:
.
故函数f(x)的周期为2.
由x∈(0,1)时,f(x)=2x+
| 1 |
| 5 |
| 5 |
| 4 |
| 5 |
| 4 |
| 1 |
| 5 |
| 5 |
| 4 |
| 1 |
| 5 |
| 29 |
| 20 |
故答案为:
| 29 |
| 20 |
点评:本题主要考查函数的奇偶性、周期性,求函数的值,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
直线
x+y-b=0截圆x2+y2-4y=0所得的劣弧所对的圆心角为
,则实数b的值是( )
| 3 |
| 2π |
| 3 |
A、2+2
| ||
| B、4 | ||
C、2±2
| ||
| D、0或4 |
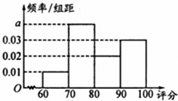 为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.
为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.