题目内容
已知等差数列{an}的前n项和为Sn,n∈N+,且点(2,a2),(a7,S3)均在直线x-y+1=0上
(1)求数列{an}的通项公式an,及前n项和Sn;
(2)若bn=
,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式an,及前n项和Sn;
(2)若bn=
| 1 |
| 2(Sn-n) |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)设等差数列{an}的公差为d,由于点(2,a2),(a7,S3)均在直线x-y+1=0上,可得2-a2+1=0,a7-S3+1=0,根据等差数列的通项公式及其前n项和公式即可得出;
(2)由bn=
=
-
.利用“裂项求和”即可得出.
(2)由bn=
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(1)设等差数列{an}的公差为d,
∵点(2,a2),(a7,S3)均在直线x-y+1=0上,
∴2-a2+1=0,a7-S3+1=0,
∴a2=3,a7-a3-a2-a1+1=0,
∴a1+d=3,a1+6d-(a1+2d)-3-a1+1=0,
即a1+d=3,4d-a1=2.
∴d=1,a1=2.
∴an=2+(n-1)=n+1.
∴Sn=
=
.
(2)bn=
=
=
-
.
∴数列{bn}的前n项和Tn=(1-
)+(
-
)+…+(
-
)=1-
=
.
∵点(2,a2),(a7,S3)均在直线x-y+1=0上,
∴2-a2+1=0,a7-S3+1=0,
∴a2=3,a7-a3-a2-a1+1=0,
∴a1+d=3,a1+6d-(a1+2d)-3-a1+1=0,
即a1+d=3,4d-a1=2.
∴d=1,a1=2.
∴an=2+(n-1)=n+1.
∴Sn=
| n(2+n+1) |
| 2 |
| n2+3n |
| 2 |
(2)bn=
| 1 |
| 2(Sn-n) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴数列{bn}的前n项和Tn=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查了“裂项求和”、等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
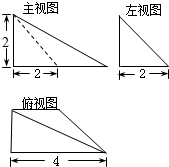 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )| A、2 | B、4 | C、6 | D、12 |
在△ABC中,AB=4,AC=3,∠A=60°,点H是△ABC的垂心,设存在实数λ,μ,使
=λ
+μ
,则( )
| AH |
| AB |
| AC |
A、λ=
| ||||
B、λ=
| ||||
C、λ=
| ||||
D、λ=
|
若函数y=f(2x+1)是偶函数,则函数y=f(2x)的图象的对称轴方程是( )
| A、x=-1 | ||
B、x=-
| ||
C、x=
| ||
| D、x=1 |