题目内容
已知数列{an}满足a1=1,an+1=
an,n∈N*,其前n项和为Sn,则( )
| 2 |
| 3 |
| A、Sn=2an-1 |
| B、Sn=3an-2 |
| C、Sn=4-3an |
| D、Sn=3-2an |
考点:等比数列的前n项和,数列递推式
专题:等差数列与等比数列
分析:根据条件判断数列{an}是等比数列,求出对应的通项公式和前n项和,即可得到结论
解答:
解:∵数列{an}满足a1=1,an+1=
an,
∴数列{an}是首项a1=1,公比q=
的等比数列,
则an=(
)n-1,Sn=
=3-3•(
)n=3-3•
(
)n-1=3-2•(
)n-1=3-2an,
故选:B
| 2 |
| 3 |
∴数列{an}是首项a1=1,公比q=
| 2 |
| 3 |
则an=(
| 2 |
| 3 |
1-(
| ||
1-
|
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
故选:B
点评:本题主要考查等比数列的判断以及等比数列的通项公式和前n项和公式的应用.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
若实数x,y满足约束条件
,则z=x-y的最大值是( )
|
| A、-1 | B、0 | C、1 | D、2 |
| ∫ | 2 -2 |
| A、0 | B、1 | C、8 | D、16 |
已知cosθ=-
,θ∈(
,π),则tanθ等于( )
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
经过两直线x+3y-10=0和3x-y=0的交点,且和原点相距为1的直线的条数为( )
| A、0 | B、1 | C、2 | D、3 |
不等式(x-2)(x+5)>0的解集为( )
| A、{x|-5<x<2} |
| B、{x|x<-2或x>5} |
| C、{x|-2<x<5} |
| D、{x|x<-5或x>2} |
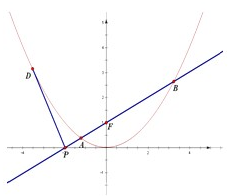 抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.
抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.