题目内容
已知A是抛物线x2=24y上的一点,且点A到抛物线准线的距离是10,则点A的坐标为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等,进而利用点到直线的距离求得x的值,代入抛物线方程求得y值,即可得到所求点的坐标.
解答:
解:∵抛物线方程为y2=4x,x2=24y
∴焦点为F(0,6),准线为l:y=-6
∵抛物线x2=24y上一点A到抛物线准线的距离是10,
∴即y+6=10,解之得y=4,
代入抛物线方程求得x=±4
,
∴点A坐标为:(4
,4)或(-4
,4).
故答案为:(4
,4)或(-4
,4).
∴焦点为F(0,6),准线为l:y=-6
∵抛物线x2=24y上一点A到抛物线准线的距离是10,
∴即y+6=10,解之得y=4,
代入抛物线方程求得x=±4
| 6 |
∴点A坐标为:(4
| 6 |
| 6 |
故答案为:(4
| 6 |
| 6 |
点评:本题主要考查了抛物线的简单性质.在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )| A、(6,10) |
| B、(8,12) |
| C、[6,8] |
| D、[8,12] |
如图是函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<
)的图象,则其解析式是( )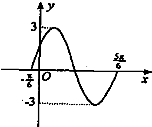
| π |
| 2 |

A、y=3sin(2x+
| ||
B、y=3sin(2x+
| ||
C、y=3sin(2x-
| ||
D、y=3sin(2x+
|