题目内容
椭圆
+
=1（a＞b＞0），F1，F2为椭圆的两个焦点且F1，F2到直线
+
=1的距离之和为
b，则离心率e= ．
| x2 |
| a2 |
| y2 |
| b2 |
| x |
| a |
| y |
| b |
| 3 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：求出两焦点的坐标，根据点到直线的距离公式求出两焦点到直线的距离和，得出a，b的关系，从而求离心率．
解答：
解：直线
+
=1可化为：bx+ay-ab=0，
由椭圆
+
=1（a＞b＞0）得，
F1（-c，0），F2（c，0），
∴F1，F2到直线
+
=1的距离之和为
=
b，
化简得：a=
b，
∴e=
=
=
=
．
故答案为：
．
| x |
| a |
| y |
| b |
由椭圆
| x2 |
| a2 |
| y2 |
| b2 |
F1（-c，0），F2（c，0），
∴F1，F2到直线
| x |
| a |
| y |
| b |
| |-bc-ab|+|bc-ab| | ||
|
| 3 |
化简得：a=
| 3 |
∴e=
| c |
| a |
| ||
| a |
| ||
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题主要考查椭圆的离心率的求法，点到直线的距离公式．
练习册系列答案
相关题目
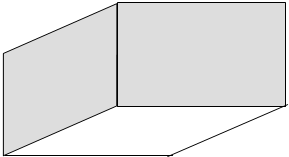如图，用一块长为2米，宽为1米的矩形木板，在教室的墙角处围出一个直三棱柱的储物角（使木板垂直于地面的两边与墙面贴紧），试问应怎样围才能使储物角的容积最大？并求出这个最大值．下列结论错误的是（ ）
| A、命题p：“?x∈R，使得x2+x+1＜0”，则￢P：?x∈R，x2+x+1≥0” | ||||
| B、“x=4”是“x2-3x-4=0”的充分非必要条件 | ||||
| C、数列2，5，11，20，x，47，…中的x=32 | ||||
D、已知a，b∈R+，2a+b=1，则
|