题目内容
已知-1≤x≤1,求函数y=2x+2-3•4x的值域.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:令t=2x,则由题意可得 t∈[
,2],函数y=2x+2-3•4x =4t-3t2=-3(t-
)2+
,再利用二次函数的性质求得函数的值域.
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
解答:
解:令t=2x,∵-1≤x≤1,∴t∈[
,2],
函数y=2x+2-3•4x =4t-3t2=-3(t-
)2+
,故当t=
时,函数y取得最大值为
,
当t=2时,函数y取得最小值为-4,
故函数的值域为[-4,
].
| 1 |
| 2 |
函数y=2x+2-3•4x =4t-3t2=-3(t-
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
当t=2时,函数y取得最小值为-4,
故函数的值域为[-4,
| 4 |
| 3 |
点评:本题主要考查指数函数的定义域和值域,二次函数的性质应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线(3λ+1)x+(1-λ)y+6-6λ=0与不等式组
表示的平面区域有公共点,则实数λ的取值范围是( )
|
A、(-∞,-
| ||
B、,(-
| ||
| C、(1,9) | ||
D、(-∞,-
|
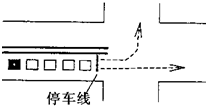 如图,一辆车要通过某十字路口,直行时前方刚好由绿灯转为红灯.该车前面已有4辆车依次在同一车道上排队等候(该车道只可以直行或左转行驶).已知每辆车直行的概率为
如图,一辆车要通过某十字路口,直行时前方刚好由绿灯转为红灯.该车前面已有4辆车依次在同一车道上排队等候(该车道只可以直行或左转行驶).已知每辆车直行的概率为