题目内容
已知f(x)=a-
是奇函数,则f(x)的值域为 .
| 1 |
| 3x-1 |
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:运用奇函数的定义,求得a,再讨论x>0,x<0时f(x)的范围,注意运用指数函数的单调性,即可得到值域.
解答:
解:f(x)=a-
是奇函数,
则f(-x)+f(x)=0,
即有a-
+a-
=0,
即2a=
+
=-1,
解得,a=-
,
则f(x)=-
-
,
由于x≠0,则当x>0时,3x>1,
>0,
-
<0,则f(x)<-
,
由于f(x)为奇函数,则x<0时,f(x)>
.
则f(x)的值域为(-∞,-
)∪(
,+∞)
故答案为:(-∞,-
)∪(
,+∞).
| 1 |
| 3x-1 |
则f(-x)+f(x)=0,
即有a-
| 1 |
| 3-x-1 |
| 1 |
| 3x-1 |
即2a=
| 3x |
| 1-3x |
| 1 |
| 3x-1 |
解得,a=-
| 1 |
| 2 |
则f(x)=-
| 1 |
| 2 |
| 1 |
| 3x-1 |
由于x≠0,则当x>0时,3x>1,
| 1 |
| 3x-1 |
-
| 1 |
| 3x-1 |
| 1 |
| 2 |
由于f(x)为奇函数,则x<0时,f(x)>
| 1 |
| 2 |
则f(x)的值域为(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查函数的奇偶性的判断和运用,考查指数函数的单调性和运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
函数y=cos2ax-sin2ax的最小正周期为π,则a的值是( )
| A、-1 | B、1 | C、2 | D、±1 |
直线x-y+2=0的倾斜角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知复数z=
,i是虚数单位,则复数z的虚部是( )
| 1+2i |
| 3-i |
A、
| ||
B、
| ||
C、
| ||
D、
|
若复数z=
,则z的实部为( )
| i |
| 1-i |
A、
| ||
B、
| ||
C、
| ||
D、-
|
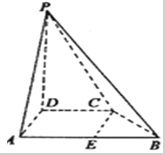 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.