题目内容
12．设Sn为等比数列{an}的前n项和，且8a3+a6=0，则$\frac{S_4}{S_2}$=（ ）| A． | -11 | B． | -8 | C． | 5 | D． | 11 |
分析 利用等比数列的通项公式及其前n项和公式即可得出．
解答 解：设等比数列{an}的公比为q，
∵8a3+a6=0，
∴a3（8+q3）=0，
解得q=-2．
则$\frac{S_4}{S_2}$=$\frac{\frac{{a}_{1}[1-（-2）^{4}]}{1-（-2）}}{\frac{{a}_{1}[1-（-2）^{2}]}{1-（-2）}}$=$\frac{1-16}{1-4}$=5，
故选：C．
点评 本题考查了等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
2．命题“若α=0，则sinα＜cosα”的否命题是（ ）
| A． | 若α=0，则sinα≥cosα | B． | 若sinα＜cosα，则α≠0 | ||
| C． | 若α≠0，则sinα≥cosα | D． | 若sinα≥cosα，则α≠0 |
20．下列计算正确的是（ ）
| A． | $\sqrt{{{（{m-n}）}^2}}=m-n$ | B． | log23×log25=log215 | ||
| C． | 210-29=29 | D． | ${（{-\frac{125}{27}}）^{\frac{2}{3}}}=-\frac{25}{9}$ |
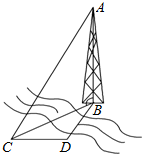如图，测量河对岸的塔高AB时，选与塔底B在同一水平面内的两个测点C与D，在D点测得塔在北偏东30°方向，然后向正西方向前进10米到达C，测得此时塔在北偏东60°方向．并在点C测得塔顶A的仰角为60°，则塔高AB=30米．