题目内容
5. 如图是幂函数$y={x^{α_i}}$(αi>0,i=1,2,3,4,5)在第一象限内的图象,其中α1=3,α2=2,α3=1,${α_4}=\frac{1}{2}$,${α_5}=\frac{1}{3}$,已知它们具有性质:
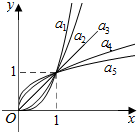
如图是幂函数$y={x^{α_i}}$(αi>0,i=1,2,3,4,5)在第一象限内的图象,其中α1=3,α2=2,α3=1,${α_4}=\frac{1}{2}$,${α_5}=\frac{1}{3}$,已知它们具有性质:①都经过点(0,0)和(1,1); ②在第一象限都是增函数.
请你根据图象写出它们在(1,+∞)上的另外一个共同性质:α越大函数增长越快.
分析 由幂函数的图象及其性质不难得到:①α越大函数增长越快;②图象从下往上α越来越大;③函数值都大于1;④α越大越远离x轴;⑤α>1,图象下凸;⑥图象无上界;⑦当指数互为倒数时,图象关于直线y=x对称;⑧当α>1时,图象在直线y=x的上方;当0<α<1时,图象在直线y=x的下方.
从上面任取一个即可得出答案.
解答 解:①α越大函数增长越快;②图象从下往上α越来越大;③函数值都大于1;④α越大越远离x轴;⑤α>1,图象下凸;⑥图象无上界;⑦当指数互为倒数时,图象关于直线y=x对称;⑧当α>1时,图象在直线y=x的上方;当0<α<1时,图象在直线y=x的下方.
从上面任取一个即可得出答案.
故答案为:α越大函数增长越快.
点评 本题考查了幂函数的图象与性质,考查了数形结合能力、推理能力与计算能力,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15.若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在函数y=-x+4图象上的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
20.下列计算正确的是( )
| A. | $\sqrt{{{({m-n})}^2}}=m-n$ | B. | log23×log25=log215 | ||
| C. | 210-29=29 | D. | ${({-\frac{125}{27}})^{\frac{2}{3}}}=-\frac{25}{9}$ |
15.下列图形中不一定是平面图形的是( )
| A. | 三角形 | B. | 菱形 | ||
| C. | 梯形 | D. | 四边相等的四边形 |
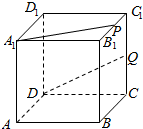 如图,在正方体ABCD-A1B1C1D1中,点P、Q分别是B1C1、CC1的中点,则直线A1P与DQ的位置关系是相交.(填“平行”、“相交”或“异面”)
如图,在正方体ABCD-A1B1C1D1中,点P、Q分别是B1C1、CC1的中点,则直线A1P与DQ的位置关系是相交.(填“平行”、“相交”或“异面”)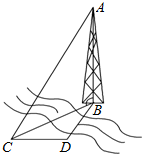 如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.
如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.