题目内容
10.关于x的方程x2+x+q=0(q∈[0,1])有实根的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
分析 由题意知本题是一个几何概型,试验包含的所有事件是q∈[0,1],而满足条件的事件是使得方程x2+x+q=0有实根的b的值,根据一元二次方程根与系数的关系得到满足条件的q的值,得到结果.
解答 解:由题意知本题是一个几何概型,
试验包含的所有事件是q∈[0,1],
而满足条件的事件是使得方程x2+x+q=0有实根的q的值,
要使方程x2+x+q=0有实根,
△=1-4bq≥0
∴b≤$\frac{1}{4}$,
∴在基本事件包含的范围之内q∈[0,$\frac{1}{4}$],
由几何概型公式得到P=$\frac{1}{4}$,
故选:C.
点评 古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
15.若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在函数y=-x+4图象上的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
2.命题“若α=0,则sinα<cosα”的否命题是( )
| A. | 若α=0,则sinα≥cosα | B. | 若sinα<cosα,则α≠0 | ||
| C. | 若α≠0,则sinα≥cosα | D. | 若sinα≥cosα,则α≠0 |
20.下列计算正确的是( )
| A. | $\sqrt{{{({m-n})}^2}}=m-n$ | B. | log23×log25=log215 | ||
| C. | 210-29=29 | D. | ${({-\frac{125}{27}})^{\frac{2}{3}}}=-\frac{25}{9}$ |
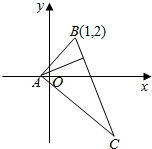 如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求:
如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求: