题目内容
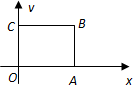 如图,正方形OABC的边长为2.
如图,正方形OABC的边长为2.(1)在其四边或内部取点P(x,y),且x,y∈Z,求事件:“|OP|>1”的概率;
(2)在其内部取点P(x,y),且x,y∈R,求事件“△POA,△PAB,△PBC,△PCO的面积均大于
| 2 |
| 3 |
考点:几何概型
专题:概率与统计
分析:(1)分析出正方形的四边和内部取点P(x,y),且x,y∈Z的全部基本事件个数,及满足“|OP|>1”的基本事件个数,代入古典概型公式可得事件“|OP|>1”的概率;
(2)求出满足条件的所有基本事件对应的平面区域Ω的面积,及满足条件“△POA,△PAB,△PBC,△PCO的面积均大于
的平面区域面积,代入几何概型公式,可得事件“△POA,△PAB,△PBC,△PCO的面积均大于
”的概率.
(2)求出满足条件的所有基本事件对应的平面区域Ω的面积,及满足条件“△POA,△PAB,△PBC,△PCO的面积均大于
| 2 |
| 3 |
| 2 |
| 3 |
解答:
解:(1)在正方形的四边和内部取点P(x,y),且x,y∈Z,所有可能的事件是
(0,0),(0,1),(0,2),(1,0),(1,1),
(1,2),(2,0),(2,1),(2,2),
其中满足|OP|>1的事件是
(0,2),(1,1),(1,2),(2,0),(2,1),(2,2),
所以满足|OP|>1的概率为
=
.
(2)在正方形内部取点,其总的事件包含的区域面积为4,
由于各边长为2,所以要使△POA,△PAB,△PBC,△PCO的面积均大于
,
应该三角形以正方形的边长为底边的高大于
,
所以这个区域为每个边长从两端各去掉
后剩余的正方形,
其面积为
×
=
,
所以满足条件的概率为
.
(0,0),(0,1),(0,2),(1,0),(1,1),
(1,2),(2,0),(2,1),(2,2),
其中满足|OP|>1的事件是
(0,2),(1,1),(1,2),(2,0),(2,1),(2,2),
所以满足|OP|>1的概率为
| 6 |
| 9 |
| 2 |
| 3 |
(2)在正方形内部取点,其总的事件包含的区域面积为4,
由于各边长为2,所以要使△POA,△PAB,△PBC,△PCO的面积均大于
| 2 |
| 3 |
应该三角形以正方形的边长为底边的高大于
| 2 |
| 3 |
所以这个区域为每个边长从两端各去掉
| 2 |
| 3 |
其面积为
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
所以满足条件的概率为
| 1 |
| 9 |
点评:本题考查的知识点是几何概型,及古典概型,其中求出所有基本事件个数(对应区域面积)和满足条件的基本事件个数(对应区域面积)是解答的关键.

练习册系列答案
相关题目
已知圆M方程:x2+(y+1)2=4,圆N的圆心(2,1),若圆M与圆N交于A B两点,且|AB|=2
,则圆N方程为( )
| 2 |
| A、(x-2)2+(y-1)2=4 |
| B、(x-2)2+(y-1)2=20 |
| C、(x-2)2+(y-1)2=12 |
| D、(x-2)2+(y-1)2=4或(x-2)2+(y-1)2=20 |
已知集合A={x|x2+4x-12<0},B={x|2x>2},则A∩B=( )
| A、{x|x<6} |
| B、{x|1<x<2} |
| C、{x|-6<x<2} |
| D、{x|x<2} |
cos300°等于( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知F1,F2是两个定点,点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点,并且PF1⊥F2,e1和e2分别是上述椭圆和双曲线的离心力,则有( )
A、
| ||||
B、
| ||||
| C、e12+e22=4 | ||||
| D、e12+e22=2 |