题目内容
已知直线的向量参数方程为(x,y,z)=(5,0,3)+t(0,3,0),当t=
时,则对应直线上的点的坐标是( )
| 1 |
| 2 |
| A、(5,0,3) | ||||
B、(
| ||||
C、(5,
| ||||
D、(
|
考点:空间向量的基本定理及其意义
专题:空间向量及应用
分析:根据直线的向量参数方程,计算t=
时,对应直线上的点的坐标即可.
| 1 |
| 2 |
解答:
解:∵直线的向量参数方程为(x,y,z)=(5,0,3)+t(0,3,0),
∴当t=
时,(x,y,z)=(5,0,3)+
(0,3,0)=(5,0,3)+(0,
,0)=(5,
,3);
对应直线上的点的坐标是(5,
,3).
故选:C.
∴当t=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
对应直线上的点的坐标是(5,
| 3 |
| 2 |
故选:C.
点评:本题考查了空间向量的几何意义以及应用问题,是基础题目.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
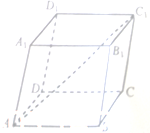
在平行六面体ABCD-A1B1C1D1中,
=x
+2y
+3z
,则x+y+z=( )
| AC1 |
| AB |
| AD |
| AA1 |

A、
| ||
B、
| ||
C、
| ||
D、
|
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
的切线,切点为E,延长FE交双曲线右支于点P,若E为线段PF的中点,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A、100 cm3 |
| B、108 cm3 |
| C、84 cm3 |
| D、92 cm3 |
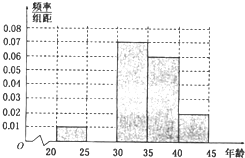 在某市“创建文明城市”活动中,对800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,据此估计这800名志愿者年龄在[25,30)的人数为
在某市“创建文明城市”活动中,对800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,据此估计这800名志愿者年龄在[25,30)的人数为