题目内容
已知数列{an}满足a1=1,a2=1,an+2=an+1+an,则a6= .
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:根据数列{an}满足a1=1,an+2=an+1+an,一步一步的求a6.
解答:
解:因为数列{an}满足a1=1,a2=1,an+2=an+1+an,
a3=a2+a1=1+1=2,
a4=a3+a2=2+1=3,
a5=a4+a3=3+2=5,
a6=a5+a4=5+3=8.
故答案为:8
a3=a2+a1=1+1=2,
a4=a3+a2=2+1=3,
a5=a4+a3=3+2=5,
a6=a5+a4=5+3=8.
故答案为:8
点评:本题主要考查利用数列递推式求值,属易题,计算细心即可.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
从甲、乙、丙三人中任选2人作代表,则甲被选中的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
用二分法求函数f(x)=ex-4x+1在区间(1,2)内零点的近似值的过程中得到f(15)<0,f(1.75)<0,f(1.875)>0,f(2)>0则函数零点落在区间( )
| A、(1.5,1.75) |
| B、(1.75,1.875) |
| C、(1.875,2) |
| D、不能确定 |
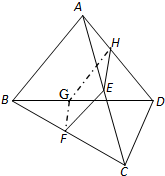 如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.
如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.