题目内容
17.已知直线l:y=kx+b,曲线C:x2+(y-1)2=1,则“b=1”是“直线l与曲线C有公共点”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 直线l与曲线C有公共点?$\frac{|b-1|}{\sqrt{{k}^{2}+1}}$≤1,化为|b-1|≤$\sqrt{{k}^{2}+1}$,即可判断出结论.
解答 解:直线l与曲线C有公共点?$\frac{|b-1|}{\sqrt{{k}^{2}+1}}$≤1,化为|b-1|≤$\sqrt{{k}^{2}+1}$.
可知:b=1时,满足上式;反之不成立,取b=$\frac{1}{2}$也可以.
∴“b=1”是“直线l与曲线C有公共点”的充分不必要条件.
故选:A.
点评 本题考查了直线与圆的位置关系、点到直线的距离公式、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下面是一段“三段论”推理过程:设函数f(x)的导数为f′(x).若函数f(x)在区间(a,b)内无极值点,则f′(x)在区间(a,b)内无零点.因为f(x)=x3在(-1,1)内无极值点,所以f′(x)=3x2在(-1,1)内无零点.以上推理中( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 结论正确 | D. | 推理形式错误 |
8.“a≥-3”是“xex+x2+ax+1>0在(0,+∞)恒成立”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
12.已知复数z=$\frac{1-i}{1+3i}$,则复数z的虚部是( )
| A. | $\frac{2}{5}$ | B. | $\frac{2}{5}$i | C. | -$\frac{2}{5}$ | D. | -$\frac{2}{5}$i |
2.从1,2,3,4,5中挑出三个不同数字组成五位数,则其中有两个数字各用两次(例如,12332)的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
6.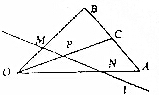 如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )
如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )
 如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )
如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |