题目内容
8.“a≥-3”是“xex+x2+ax+1>0在(0,+∞)恒成立”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 x∈(0,+∞),xex+x2+ax+1>0化为:-a<$({e}^{x}+x+\frac{1}{x})$.令f(x)=ex+x+$\frac{1}{x}$,x∈(0,+∞),利用几何画板可得图象:即可判断出结论.
解答 解:∵x∈(0,+∞),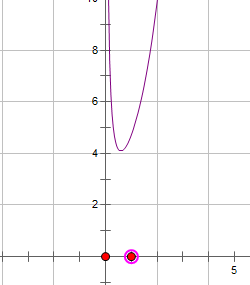
∴xex+x2+ax+1>0化为:-a<$({e}^{x}+x+\frac{1}{x})$.
令f(x)=ex+x+$\frac{1}{x}$,x∈(0,+∞),
利用几何画板可得图象:
由图象可得:f(x)min>4,
∴-a<4,
∴a>-4.
∴a≥-3是xex+x2+ax+1>0在(0,+∞)上的充分不必要条件.
故选:A.
点评 本题考查了几何画板的应用、恒成立问题的等价转化方法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.由①安梦怡是高二(21)班学生;②安梦怡是独生子女,③高二(21)班的学生都是独生子女,写一个“三段论”形式的推理,则大前提,小前提和结论分别为( )
| A. | ②①③ | B. | ③①② | C. | ①②③ | D. | ②③① |
3.已知集合M={x|-1≤x≤1},N={x|$\frac{x}{x-1}$≤0},则M∩N=( )
| A. | {x|0≤x<1} | B. | {x|0<x≤1} | C. | {x|-1≤x≤1} | D. | {x|-1≤x<1} |
13.设命题p:?x0∈(0,+∞),e${\;}^{{x}_{0}}$+x0=e,命题q:,若圆C1:x2+y2=a2与圆C2:(x-b)2+(y-c)2=a2相切,则b2+c2=2a2.那么下列命题为假命题的是( )
| A. | ¬q | B. | ¬p | C. | (¬p)∨(¬q) | D. | p∧(¬q) |
17.已知直线l:y=kx+b,曲线C:x2+(y-1)2=1,则“b=1”是“直线l与曲线C有公共点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |