题目内容
7.下面是一段“三段论”推理过程:设函数f(x)的导数为f′(x).若函数f(x)在区间(a,b)内无极值点,则f′(x)在区间(a,b)内无零点.因为f(x)=x3在(-1,1)内无极值点,所以f′(x)=3x2在(-1,1)内无零点.以上推理中( )| A. | 大前提错误 | B. | 小前提错误 | C. | 结论正确 | D. | 推理形式错误 |
分析 在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析的其大前提的形式:“若函数f(x)在区间(a,b)内无极值点,则f′(x)在区间(a,b)内无零点,不难得到结论.
解答 解:∵函数f(x)的导数为f′(x).若函数f(x)在区间(a,b)内无极值点,则f′(x)在区间(a,b)内无零点,是假命题,
∴大前提错误,
故选:A.
点评 本题考查的知识点是演绎推理的基本方法,演绎推理是一种必然性推理,演绎推理的前提与结论之间有蕴涵关系.因而,只要前提是真实的,推理的形式是正确的,那么结论必定是真实的,但错误的前提可能导致错误的结论.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
14.已知定义在R上的奇函数满足f(x+1)=-f(x),且在[0,1)上单调递增,记a=f($\frac{1}{2}$),b=f(2),c=f(3),则a,b,c的大小关系为( )
| A. | a>b=c | B. | b>a=c | C. | b>c>a | D. | a>c>b |
16.由①安梦怡是高二(21)班学生;②安梦怡是独生子女,③高二(21)班的学生都是独生子女,写一个“三段论”形式的推理,则大前提,小前提和结论分别为( )
| A. | ②①③ | B. | ③①② | C. | ①②③ | D. | ②③① |
17.已知直线l:y=kx+b,曲线C:x2+(y-1)2=1,则“b=1”是“直线l与曲线C有公共点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
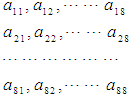 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,每一列的数都成等比数列且每列数的公比都等于q,且a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,每一列的数都成等比数列且每列数的公比都等于q,且a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.