题目内容
15. 已知正三角形A1A2A3,A4、A5、A6分别是所在棱的中点,如图,则当1≤i≤6,1≤j≤6,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$的不同数量积的个数为9.
已知正三角形A1A2A3,A4、A5、A6分别是所在棱的中点,如图,则当1≤i≤6,1≤j≤6,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$的不同数量积的个数为9.
分析 以A1A2所在直线为x轴,中点A4为坐标原点,建立直角坐标系,可设A1(-1,0),A2(1,0),A3(0,$\sqrt{3}$),A4(0,0),A5(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),A6($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),运用向量的坐标运算和数量积的坐标表示,计算即可得到所求个数.
解答 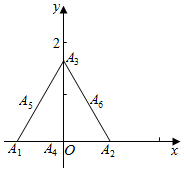 解:以A1A2所在直线为x轴,中点A4为坐标原点,建立直角坐标系,
解:以A1A2所在直线为x轴,中点A4为坐标原点,建立直角坐标系,
可设A1(-1,0),A2(1,0),A3(0,$\sqrt{3}$),
A4(0,0),A5(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),A6($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
可得$\overrightarrow{{A}_{1}{A}_{2}}$=(2,0),
若i=1,则$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$=2(${x}_{{A}_{j}}$+1),
可得4,2,2,1,3;
若i=2,则$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$=2(${x}_{{A}_{j}}$-1),
可得-4,-2,-2,-3,-1;
若i=3,则$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$=2(${x}_{{A}_{j}}$),
可得-2,2,0,-1,1;
若i=4,则$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$=2(${x}_{{A}_{j}}$),
可得-2,2,0,-1,1;
若i=5,则$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$=2(${x}_{{A}_{j}}$+$\frac{1}{2}$),
可得-1,3,1,1,2;
若i=6,则$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$=2(${x}_{{A}_{j}}$-$\frac{1}{2}$),
可得-3,1,-1,-1,-2.
综上可得取值有±1,±2,±3,±4,0共9个.
点评 本题考查向量的数量积的坐标表示,考查运算能力,属于中档题.

| A. | $\frac{5}{3}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
| A. | (1,-$\frac{1}{2}$) | B. | (-1,-$\frac{1}{2}$) | C. | (1,-1) | D. | (-1,-1) |
| A. | 24 | B. | 27 | C. | 15 | D. | 54 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $-\frac{1}{5}$ | D. | $-\frac{1}{2}$ |