题目内容
16.在Rt△ABC中,CA=4,CB=3,M,N是斜边AB上的两个动点,且MN=2,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围为( )| A. | $[2,\frac{5}{2}]$ | B. | [4,6] | C. | $[\frac{119}{25},\frac{48}{5}]$ | D. | $[\frac{144}{25},\frac{53}{5}]$ |
分析 可以C为坐标原点,CA为x轴建立平面直角坐标系,可得出A,B点的坐标,进而写出直线AB的方程,从而可设$M(a,3-\frac{3}{4}a),N(b,3-\frac{3}{4}b)$,根据MN=2即可得出$b=a+\frac{8}{5}$,进而求出$0≤a≤\frac{12}{5}$,并求出$\overrightarrow{CM}•\overrightarrow{CN}=\frac{25}{16}{a}^{2}-2a+\frac{27}{5}$,这样配方即可求出$\overrightarrow{CM}•\overrightarrow{CN}$的最小、最大值,即得出其取值范围.
解答 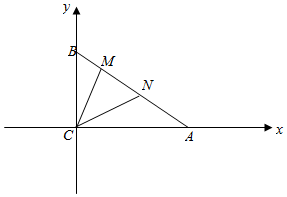 解:如图,以C为坐标原点,CA为x轴建立平面坐标系,则:
解:如图,以C为坐标原点,CA为x轴建立平面坐标系,则:
A(4,0),B(0,3);
直线AB的方程为$\frac{x}{4}+\frac{y}{3}=1$,即$y=3-\frac{3}{4}x$;
设$M(a,3-\frac{3}{4}a),N(b,3-\frac{3}{4}b)$,且0≤a≤4,0≤b≤4,且a<b;
∵MN=2;
∴$(a-b)^{2}+\frac{9}{16}(a-b)^{2}=4$;
∴$(a-b)^{2}=\frac{64}{25}$;
∴$b-a=\frac{8}{5}$;
∴$b=a+\frac{8}{5}$;
∴$0≤a≤\frac{12}{5}$;
$\overrightarrow{CM}•\overrightarrow{CN}=ab+(3-\frac{3}{4}a)(3-\frac{3}{4}b)$
=$\frac{25}{16}ab-\frac{9}{4}(a+b)+9$
=$\frac{25}{16}{a}^{2}-2a+\frac{27}{5}$
=$\frac{25}{16}(a-\frac{16}{25})^{2}+\frac{119}{25}$,$0≤a≤\frac{12}{5}$;
∴$a=\frac{16}{25}$时,取最小值$\frac{119}{25}$;
$a=\frac{12}{5}$时,取最大值$\frac{48}{5}$;
∴$\overrightarrow{CM}•\overrightarrow{CN}$的取值范围为$[\frac{119}{25},\frac{48}{5}]$.
故选C.
点评 考查通过建立坐标系,利用坐标解决向量问题的方法,直线的斜截式方程,数量积的坐标运算,以及配方求二次函数最值的方法.

| A. | 1 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
| A. | 3$\sqrt{13}$ | B. | 9$\sqrt{5}$ | C. | 14 | D. | 21 |