题目内容
2．已知函数f（x）=（x-a）（x-b）（其中a＞b）的图象如图所示，则函数g（x）=b+logax的图象大致是（ ）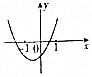
| A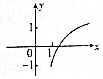． |  | B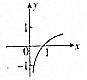． |  | C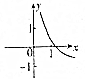． |  | D． |  |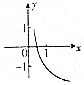
分析 由函数f（x）=（x-a）（x-b）（其中a＞b）的图象得到0＜a＜1，b＜-1，从而函数g（x）=b+logax是减函数，函数g（x）=b+logax的图象与x轴的交点位于（0，）与（1，0）之间．
解答 解：函数f（x）=（x-a）（x-b）（其中a＞b）的图象如图所示，
∴0＜a＜1，b＜-1，
∴0＜x＜1，∴函数g（x）=b+logax是减函数，
∵b＜-1，∴函数g（x）=b+logax的图象与x轴的交点位于（0，0）与（1，0）之间，
故选：D．
点评 本题考查函数图象的判断，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
13．设函数f（x），g（x）的定义域为R，且f（x）是奇函数，g（x）是偶函数，则下列结论正确的是（ ）
| A． | f（x）•g（x）是偶函数 | B． | f（x）+x2是奇函数 | C． | f（x）-sinx是奇函数 | D． | g（x）+2x是奇函数 |
10．已知定义在R上的函数满足f（1）=2，且f（x）的导数f′（x）在R上恒有f′（x）＜1（x∈R），则不等式f（x）＜x+1的解集为（ ）
| A． | （1，+∞） | B． | （-∞，-1） | C． | （-1，1） | D． | （-∞，1）∪（1，+∞） |
17．已知函数f（x）的定义域为[-1，5]，在同一坐标系下，函数y=f（x）的图象与直线x=1的交点个数为（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 0个或者2个 |
7．已知函数f（x）=$\left\{\begin{array}{l}{-lnx，x≥0}\\{（\frac{1}{2}）^{x}，x＜0}\end{array}\right.$则f（f（e））=2．
12．等差数列{an}的前n项和为Sn，且S5=6，a2=1，则公差d等于（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{6}{5}$ | D． | 2 |