题目内容
已知函数f(x)=x2-2ax+2,当x∈[-1,+∞)时,f(x)≥a恒成立,则a的取值范围________.
[-3,1]
解析 因为f(x)=(x-a)2+2-a2,
所以此二次函数图象的对称轴为x=a.
①当a∈(-∞,-1)时,f(x)在[-1,+∞)上单调递增,
所以f(x)min=f(-1)=2a+3.
要使f(x)≥a恒成立,只需f(x)min≥a,
即2a+3≥a,解得a≥-3,即-3≤a<-1.
②当a∈[-1,+∞)时,f(x)min=f(a)=2-a2.
要使f(x)≥a恒成立,只需f(x)min≥a,
即2-a2≥a,解得-2≤a≤1,即-1≤a≤1.
综上,实数a的取值范围为[-3,1].

练习册系列答案
相关题目
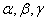 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: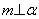 ,
,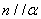 ,则
,则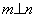 ②若
②若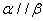 ,
,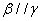 ,
,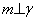
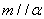 ,
,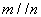 ④若
④若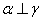 ,
, ,则
,则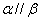
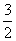 x-m=0在x∈[-1,1]上有实根,则m的取值范围是________.
x-m=0在x∈[-1,1]上有实根,则m的取值范围是________.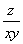 取得最小值时,x+2y-z的最大值为________.
取得最小值时,x+2y-z的最大值为________.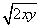 ≤λ(x+y)恒成立,则实数λ的最小值为________.
≤λ(x+y)恒成立,则实数λ的最小值为________. 为右焦点,A为长轴的左端点,P点为该椭圆上的动点,则能够使
为右焦点,A为长轴的左端点,P点为该椭圆上的动点,则能够使 的P点的个数为 A、4 B、3 C、2 D、1
的P点的个数为 A、4 B、3 C、2 D、1