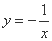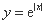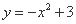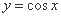题目内容
给定两个命题,命题p:对任意实数x都有ax2>-ax-1恒成立;命题q:关于x的方程x2-x+a=0有实数根.若“p∨q”为真命题,“p∧q”为假命题,则实数a的取值范围为________.
(-∞,0)∪( ,4)
,4)
解析 若p为真命题,则a=0或
即0≤a<4;
若q为真命题,则(-1)2-4a≥0,即a≤ .
.
因为“p∨q”为真命题,“p∧q”为假命题,
所以p,q中有且仅有一个为真命题.
若p真q假,则 <a<4;
<a<4;
若p假q真,则a<0.
综上,实数a的取值范围为(-∞,0)∪( ,4).
,4).

练习册系列答案
相关题目
下列函数中,既是偶函数又在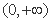 单调递增的函数是 ( )
单调递增的函数是 ( )
| (A) | (B) | (C) | (D) |

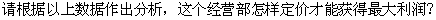
 ,四边形ABCD是正方形,
,四边形ABCD是正方形,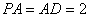 ,
,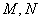 分别是AB、PC的中点.
分别是AB、PC的中点. 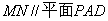
 的余弦值
的余弦值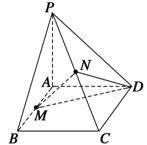
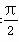 ”的________条件.
”的________条件.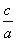 >
>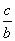 ”的逆否命题;
”的逆否命题;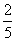 ,求y=2x-5x2的最大值;
,求y=2x-5x2的最大值;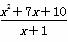 (x>-1)的最小值.
(x>-1)的最小值.