题目内容
已知圆C:(x-3)2+(y-4)2=1和两点A(-a,1),B(a,-1),且a>0,若圆C上存在点P,使得∠APB=90°,则a的最大值为.( )
| A、6 | ||
B、
| ||
C、2
| ||
| D、5 |
考点:直线与圆的位置关系
专题:直线与圆
分析:设P(m,n)在圆C上,由题意可得
•
=0,求得a2=m2+n2-1=|OP|2-1,根据|OP|的最大值是|OC|+1,可得a的最大值.
| AP |
| BP |
解答:
解:圆C:(x-3)2+(y-4)2=1的圆心C(3,4),半径r=1,
设P(m,n)在圆C上,则
=(m+a,n-1),
=(m-a,n+1),
∵∠APB=90°,∴
⊥
,
•
=(m+a)(m-a)+(n+1)(n-1)=0,
∴a2=m2+n2-1=|OP|2-1,
∴a=
,∴当|OP|取得最大值时,a取得最大值.
由于|OP|的最大值是|OC|+1=5+1=6,故a的最大值为
=
,
故选:B.
设P(m,n)在圆C上,则
| AP |
| BP |
∵∠APB=90°,∴
| AP |
| BP |
| AP |
| BP |
∴a2=m2+n2-1=|OP|2-1,
∴a=
| |OP|2-1 |
由于|OP|的最大值是|OC|+1=5+1=6,故a的最大值为
| 36-1 |
| 35 |
故选:B.
点评:本题主要考查直线和圆的位置关系,求参数的最大值的方法,解题时要认真审题,注意圆的性质的合理运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设二项式(x-
)4的展开式中常数项为A,则A=( )
| 1 | |||
|
| A、-6 | B、-4 | C、4 | D、6 |



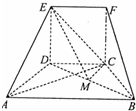 在如图所示的几何体中,四边形CDEF为正方形,ABCD为等腰梯形,AB∥CD,BD=2
在如图所示的几何体中,四边形CDEF为正方形,ABCD为等腰梯形,AB∥CD,BD=2