题目内容
14.已知椭圆C经过点A(2,3)、B(4,0),对称轴为坐标轴,焦点F1、F2在x轴上.(Ⅰ)求椭圆C的方程;
(Ⅱ)求∠F1AF2的角平分线所在的直线l与椭圆C的另一个交点的坐标.
分析 (Ⅰ)设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,a>b>0,利用待定系数法能求出椭圆C的方程.
(Ⅱ)直线AF1的方程为3x-4y+6=0,求出直线l的方程为2x-y-x=0,与椭圆联立,得19x2-16x-44=0,由此利用韦达定理能求出直线l与椭圆C的另一个交点坐标.
解答 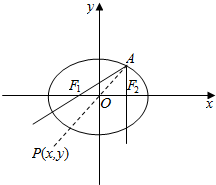 解:(Ⅰ)∵椭圆C经过点A(2,3)、B(4,0),对称轴为坐标轴,焦点F1、F2在x轴上,
解:(Ⅰ)∵椭圆C经过点A(2,3)、B(4,0),对称轴为坐标轴,焦点F1、F2在x轴上,
∴设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,a>b>0,
则$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{\frac{16}{{a}^{2}}=1}\end{array}\right.$,解得a2=16,b2=12,
∴椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.
(Ⅱ)∵椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$,
∴F1(-2,0),F2(2,0),则直线AF1的方程为y=$\frac{3}{4}(x+2)$,即3x-4y+6=0,
直线AF2的方程为x=2,由点A在椭圆C上的位置得直线l的斜率为正数,
设P(x,y)为直线l上一点,则$\frac{|3x-4y+6|}{9+16}$=|x-2|,
解得2x-y-1=0或x+2y-8=0(斜率为负,舍),
∴直线l的方程为2x-y-x=0,
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\\{2x-y-1=0}\end{array}\right.$,整理,得19x2-16x-44=0,
设直线l与椭圆C的另一个交点为M(x0,y0),
则有${x}_{0}+2=\frac{16}{9}$,解得${x}_{0}=-\frac{22}{9}$,${y}_{0}=2{x}_{0}-1=-\frac{63}{19}$,
∴直线l与椭圆C的另一个交点坐标为(-$\frac{22}{19}$,-$\frac{63}{19}$).
点评 本题考查椭圆方程的求法,考查直线与椭圆的另一个交点坐标的求法,是中档题,解题时要认真审题,注意椭圆性质、韦达定理的合理运用.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
| A. | $\sqrt{15}$ | B. | $\sqrt{14}$ | C. | $\sqrt{13}$ | D. | $\sqrt{12}$ |
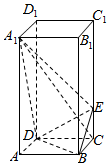 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.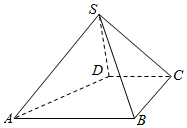 如图,四棱锥S-ABCD中,BC⊥CD,AB∥平面SCD,又SD⊥平面SAB,且AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,BC⊥CD,AB∥平面SCD,又SD⊥平面SAB,且AB=BC=2,CD=SD=1.