题目内容
9.已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{1}{2}$,经过左焦点F1(-1,0)的直线l与椭圆G相交于A,B两点,与y轴相交于C点,且点C在线段AB上.(Ⅰ)求椭圆G的方程;
(Ⅱ)若|AF1|=|CB|,求直线l的方程.
分析 (Ⅰ)设椭圆焦距为2c,运用离心率公式和a,b,c的关系,即可得到椭圆方程;
(Ⅱ)由题意可知直线l斜率存在,可设直线l:y=k(x+1),代入椭圆方程,运用韦达定理和向量共线的坐标表示,解方程即可得到所求方程.
解答 解:(Ⅰ)设椭圆焦距为2c,
由已知可得$\frac{c}{a}=\frac{1}{2}$,且c=1,
所以a=2,即有b2=a2-c2=3,
则椭圆G的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(Ⅱ)由题意可知直线l斜率存在,可设直线l:y=k(x+1),
由$\left\{{\begin{array}{l}{y=k(x+1)}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$消y,并化简整理得(4k2+3)x2+8k2x+4k2-12=0,
由题意可知△>0,设A(x1,y1),B(x2,y2),
则${x_1}+{x_2}=\frac{{-8{k^2}}}{{4{k^2}+3}},{x_1}{x_2}=\frac{{4{k^2}-12}}{{4{k^2}+3}}$,
因为点C,F1都在线段AB上,且|AF1|=|CB|,
所以$\overrightarrow{A{F_1}}=\overrightarrow{CB}$,即(-1-x1,-y1)=(x2,y2-yC),
所以-1-x1=x2,即x1+x2=-1,
所以${x_1}+{x_2}=\frac{{-8{k^2}}}{{4{k^2}+3}}=-1$,
解得${k^2}=\frac{3}{4}$,即$k=±\frac{{\sqrt{3}}}{2}$.
所以直线l的方程为$y=\frac{{\sqrt{3}}}{2}(x+1)$或$y=-\frac{{\sqrt{3}}}{2}(x+1)$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式,考查直线方程和椭圆方程联立,运用韦达定理和向量共线的坐标表示,考查运算能力,属于中档题.

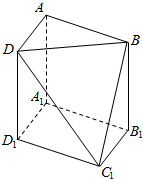 在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )
在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{3}$ | D. | $\frac{5}{2}$ |
| A. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$ | B. | $\frac{{x}^{2}}{36}+\frac{{y}^{2}}{27}=1$ | C. | $\frac{{x}^{2}}{36}+\frac{{y}^{2}}{9}=1$ | D. | $\frac{{y}^{2}}{36}+\frac{{x}^{2}}{27}=1$ |
 如图,已知平面直角坐标系中点Q(2,0)和圆O:x2+y2=1,动点M到圆O的切线长|MN|与|MQ|相等,求动点M的轨迹方程.
如图,已知平面直角坐标系中点Q(2,0)和圆O:x2+y2=1,动点M到圆O的切线长|MN|与|MQ|相等,求动点M的轨迹方程.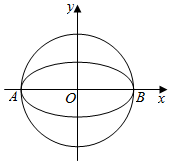 如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上. 如图,棱柱ABCD-A1B1C1D1的底面是菱形,∠DAB=60°,AA1⊥面ABCD,且AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.
如图,棱柱ABCD-A1B1C1D1的底面是菱形,∠DAB=60°,AA1⊥面ABCD,且AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.