题目内容
6.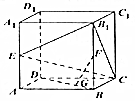 如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.
如图,在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB.(Ⅰ)求三棱锥B1-EBC的体积;
(Ⅱ)作出长方体ABCD-A1B1C1D1被平面EB1C所截的截面(只要作出,说明结果即可);
(Ⅲ)求证:GF∥平面EB1C.
分析 (Ⅰ)求出${S}_{△{B}_{1}BC}=\frac{1}{2}B{B}_{1}×BC=1$,点E到平面B1BC的距离为AB=$\sqrt{3}$,由此能求出三棱锥B1-EBC的体积.
(Ⅱ)取AD的中点M,连结EM,MC,则EMCB1是长方体ABCD-A1B1C1D1被平面EB1C所截的截面.
(Ⅲ)设MC∩DB=N,连结B1N,推导出FG∥B1N,由此能证明GF∥平面EB1C.
解答 解:(Ⅰ)∵在长方体ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,
E、F分别是AA1和BB1的中点,G是DB上的点,且DG=2GB,
∴${S}_{△{B}_{1}BC}=\frac{1}{2}B{B}_{1}×BC=1$,
点E到平面B1BC的距离为AB=$\sqrt{3}$,
∴三棱锥B1-EBC的体积V=$\frac{1}{3}$×${S}_{△{B}_{1}BC}$×AB=$\frac{\sqrt{3}}{3}$.
(Ⅱ)取AD的中点M,连结EM,MC,
则EMCB1是长方体ABCD-A1B1C1D1被平面EB1C所截的截面.
证明:(Ⅲ)设MC∩DB=N,连结B1N,
依题意知AD∥BC,∴△DMN∽△BCN,
∴$\frac{DN}{BN}=\frac{DM}{BC}=\frac{1}{2}$,
又∵DG=2GB,∴DN=NG=GB,
又∵B1F=FB,∴FG∥B1N,
∵FG?平面EB1C,∴B1N?平面EB1C,
∴GF∥平面EB1C.
点评 本题考查三棱锥的体积的求法,考查截面的求法,考查线面平行的证明,是中档题,解题时要 认真审题,注意空间思维能力的培养.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
16.方程x2+$\sqrt{2}$x-1=0的解可视为函数y=x+$\sqrt{2}$与函数y=$\frac{1}{x}$的图象交点的横坐标,若x4+ax-4=0的各实根x1、x2、…、xk(k≤4)所对应的点(xi,$\frac{4}{{x}_{i}}$)(i=1,2,…,k)均在直线y=x的同一侧,则实数a的取值范围是( )
| A. | (-∞,-6) | B. | (-∞,-6)∪(6,+∞) | C. | (6,+∞) | D. | (-6,6) |
1.已知直线x=1上的点P到直线x-y=0的距离为$\sqrt{2}$,则点P的坐标为( )
| A. | (1,-1) | B. | (1,3) | C. | (1,-2)或(1,2) | D. | (1,-1)或(1,3) |
16.已知全集U={1,2,3,4,5,6,7},A={2,4,5},B={1,3,5,7},则A∩(∁UB)为( )
| A. | {1,4,6} | B. | {2,4,6} | C. | {2,4} | D. | {4} |
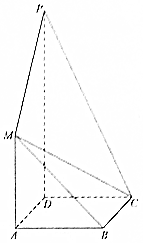 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.