题目内容
已知正三棱锥S-ABC的外接球的表面积为36π，M、N分别是SC、BC的中点，且MN⊥AM，则此三棱锥的侧棱SA= ．
考点：棱锥的结构特征
专题：计算题,空间位置关系与距离
分析：由题意可证MN⊥平面SAC，即SB⊥平面SAC，∠ASB=∠BSC=∠ASC=90°，将此三棱锥补成正方体，则它们有相同的外接球，正方体的对角线就是球的直径，由此利用外接球的表面积公式求出直径，再求出SA．
解答：
解：∵三棱锥S-ABC正棱锥，∴SB⊥AC（对棱互相垂直），MN∥SB，∴MN⊥AC
又∵MN⊥AM，AM∩AC=A，∴MN⊥平面SAC，SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°，将此三棱锥补成正方体，则它们有相同的外接球，
设SA=SB=SC=a，外接球的半径为R，则4πR2=36π，∴R=3，
∴2R=
⇒a=2
．
故答案为：2
．
又∵MN⊥AM，AM∩AC=A，∴MN⊥平面SAC，SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°，将此三棱锥补成正方体，则它们有相同的外接球，
设SA=SB=SC=a，外接球的半径为R，则4πR2=36π，∴R=3，
∴2R=
| 3a2 |
| 3 |
故答案为：2
| 3 |
点评：考查三棱锥的外接球的表面积，考查空间想象能力，三棱锥扩展为正方体，它的对角线长就是外接球的直径，是解决本题的关键．
练习册系列答案
相关题目
若x、y满足约束条件
，则z=x+2y的取值范围是（ ）
|
| A、[0，4] |
| B、[4，6] |
| C、[2，4] |
| D、[2，6] |
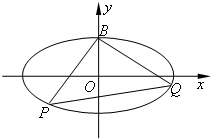已知椭圆C：
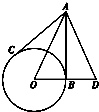如图，AB、AC为⊙O的切线，B和C是切点，延长OB到D，使BD=OB，连接AD．如果∠DAC=78°，那么∠ADO等于