题目内容
8．
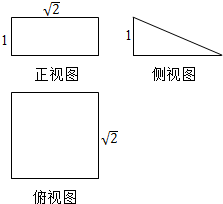一个几何体的三视图及其尺寸（单位：cm）如图所示．（1）画出该几何体的直观图；
（2）求该几何体的体积与表面积．
分析 该几何体是一个以侧视图为底面的三棱柱，
（1）利用斜二侧画法，可得几何体的直观图；
（2）代入柱体体积和表面积公式，可得答案．
解答 解：（1）画出该几何体的直观图如下图所示：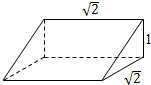
；
（2）该几何体是一个以侧视图为底面的三棱柱，
其底面面积为：$\frac{1}{2}×1×\sqrt{2}$=$\frac{\sqrt{2}}{2}$cm2，
底面周长为：（1$+\sqrt{2}+\sqrt{3}$）cm，
高为$\sqrt{2}$cm，
故几何体的体积V=$\frac{\sqrt{2}}{2}×\sqrt{2}$=1cm3；
表面积S=$\frac{\sqrt{2}}{2}$×2+（1$+\sqrt{2}+\sqrt{3}$）×$\sqrt{2}$=2+2$\sqrt{2}$+$\sqrt{6}$cm2．
点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
16．某几何体的正视图和侧视图如图所示，该几何体体积的最大值是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{2}{3}$ | D． | 1 |