题目内容
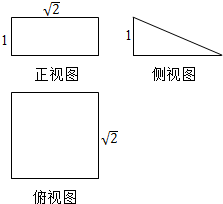
16.某几何体的正视图和侧视图如图所示,该几何体体积的最大值是( )
| A. | $\frac{1}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2}{3}$ | D. | 1 |
分析 由已知中的正视图和侧视图可得:当底面为边长为1的正方形时,该几何体体积最大,代入棱锥的体积公式,可得答案.
解答 解:由已知中的正视图和侧视图可得:
当底面为边长为1的正方形时,
该几何体体积最大,
此时V=$\frac{1}{3}$×1×1×2=$\frac{2}{3}$,
故选:C
点评 本题考查的知识点是简单空间图形的三视图,考查空间想象能力,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若纯虚数z满足(1-i)z=1+ai,则实数a等于( )
| A. | 0 | B. | -1或1 | C. | -1 | D. | 1 |
7.若命题p:?x∈R,x2-3x+5>0,则该命题的否定是( )
| A. | ?x∈R,x2-3x+5≤0 | B. | ?x∈R,x2-3x+5>0 | C. | ?x∈R,x2-3x+5<0 | D. | ?x∈R,x2-3x+5≤0 |
5.已知x与y之间的一组数据:则y与x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
| A. | (1,2) | B. | (5,2) | C. | (2,5) | D. | (2.5,5) |
6.设复数z=2+i,则复数z(1-z)的共轭复数为( )
| A. | -1-3i | B. | -1+3i | C. | 1+3i | D. | 1-3i |
 一个几何体的三视图及其尺寸(单位:cm)如图所示.
一个几何体的三视图及其尺寸(单位:cm)如图所示.