题目内容
20.函数f(x)=lnx+ax(a<0)的单调增区间为$(0,-\frac{1}{a}]$.分析 令f′(x)≥0,解得x范围即可得出.
解答 解:f(x)=lnx+ax(a<0),f′(x)=$\frac{1}{x}$+a=$\frac{a(x-\frac{1}{-a})}{x}$,
令f′(x)≥0,解得$0<x≤-\frac{1}{a}$.
∴函数f(x)=lnx+ax(a<0)的单调增区间为$(0,-\frac{1}{a}]$.
故答案为:$(0,-\frac{1}{a}]$.
点评 本题考查了利用导数研究函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于( )
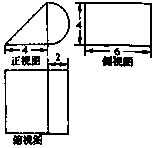

| A. | 24+6πcm3 | B. | 24+12πcm3 | C. | 48+12πcm3 | D. | 96+12πcm3 |
11.已知向量$\overrightarrow a≠\overrightarrow e$,$|\overrightarrow e|=1$,对任意t∈R,恒有$|\overrightarrow a-t\overrightarrow e|≥|\overrightarrow a-2\overrightarrow e|$,则( )
| A. | $\overrightarrow a⊥\overrightarrow e$ | B. | $\overrightarrow a⊥(\overrightarrow a-2\overrightarrow e)$ | C. | $\overrightarrow e⊥(\overrightarrow a-2\overrightarrow e)$ | D. | $(\overrightarrow a+2\overrightarrow e)⊥(\overrightarrow a-2\overrightarrow e)$ |