题目内容
7.设等比数列{an}的公比为q,前n项和为Sn,则“|q|=1”是“S6=3S2”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据等比数列的前n项和为Sn.结合充分条件和必要条件的定义进行判断.
解答 解:若q=1时,S6=6a1=3S2=3•2a1=6a1,
q=-1时,S6=3S2=0,符合题意,是充分条件;
反之也成立,
故“|q|=1”是“S6=3S2”的充要条件,
故选:C.
点评 本题主要考查充分条件和必要条件的应用,利用等比数列的性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.任意a∈R,曲线y=ex(x2+ax+1-2a)在点P(0,1-2a)处的切线l与圆C:x2+2x+y2-12=0的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上均有可能 |
17.已知f(x)=log3x,f(a)>f(2),那么a的取值范围是( )
| A. | {a|a>2} | B. | {a|1<a<2} | C. | $\{a|a>\frac{1}{2}\}$ | D. | $\{a|\frac{1}{2}<a<1\}$ |
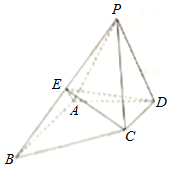 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点