题目内容
5．已知a∈{-2，0，1，3}，b∈{1，2}，则曲线ax2+by2=1为椭圆的概率是（ ）| A． | $\frac{3}{7}$ | B． | $\frac{4}{7}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{8}$ |
分析 基本事件总数n=4×2=8，利用列举法求出曲线ax2+by2=1为椭圆包含的基本事件个数，由此能求出曲线ax2+by2=1为椭圆的概率．
解答 解：∵a∈{-2，0，1，3}，b∈{1，2}，
∴基本事件总数n=4×2=8，
曲线ax2+by2=1为椭圆包含的基本事件有：（1，2），（3，1），（3，2），
共有3个，
曲线ax2+by2=1为椭圆的概率p=$\frac{3}{8}$．
故选：D．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
15．全集U={1，2，3，4，5，6}，若M={1，4}，N={2，3}，则∁U（M∪N）等于（ ）
| A． | {1，2，3，4} | B． | {3，4} | C． | {1，6} | D． | {5，6} |
13．已知函数f（x）=sin（ωx+$\frac{π}{3}$）（ω＞0），f（x）在区间（0，2]上只有一个最大值1和一个最小值-1，则实数ω的取值范围为（ ）
| A． | [$\frac{7π}{12}$，$\frac{13π}{12}$） | B． | [$\frac{π}{2}$，π） | C． | [$\frac{π}{6}$，$\frac{π}{2}$） | D． | [$\frac{π}{6}$，$\frac{π}{3}$] |
20．下列说法中正确的是（ ）
| A． | “a＞b”是“log2a＞log2b”的充要条件 | |
| B． | 若函数y=sin2x的图象向左平移$\frac{π}{4}$个单位得到的函数图象关于y轴对称 | |
| C． | 命题“在△ABC中，$A＞\frac{π}{3}$，则$sinA＞\frac{{\sqrt{3}}}{2}$”的逆否命题为真命题 | |
| D． | 若数列{an}的前n项和为${S_n}={2^n}$，则数列{an}是等比数列 |
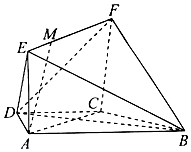如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，∠ABC=60°，四边形ACFE是矩形，且平面ACFE⊥平面ABCD，点M在线段EF上．