题目内容
若函数f（x）=ax2+bx在[b-1，2b]上是奇函数，则a+b的值为 ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：运用奇函数的定义，求解，先考虑区间，再考虑解析式．
解答：
解：∵函数f（x）=ax2+bx在[b-1，2b]上是奇函数，
∴-ax2-bx=a（-x）2+b（-x），b-1+2b=0，
a=0，b=
，
∴a+b=
，
故答案为：
．
∴-ax2-bx=a（-x）2+b（-x），b-1+2b=0，
a=0，b=
| 1 |
| 3 |
∴a+b=
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查了函数的性质，属于容易题．
练习册系列答案
相关题目
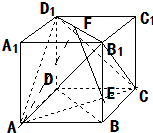如图所示，在正方形ABCD-A1B1C1D1中，E、F分别是BB1、D1B1的中点．求证：EF⊥平面B1AC．