题目内容
正项等比数列{an}中,a1=2,且a2,a1+a2,a3成等差数列.
(Ⅰ) 求数列{an}的通项公式;
(Ⅱ) 设bn=(1-
)2+a(1+
)(n∈N*),若a∈[0,2],求数列{bn}的最小项.
(Ⅰ) 求数列{an}的通项公式;
(Ⅱ) 设bn=(1-
| 2 |
| an |
| 1 |
| an |
考点:数列与不等式的综合,数列的函数特性,等差数列的通项公式
专题:等差数列与等比数列
分析:(Ⅰ) 通过a2,S2,a3成等差,求出q.推出通项公式即可.
(Ⅱ)方法一:通过
=t∈{
,
,
,…,
,…},利用二次函数的对称轴,讨论a的值,通过函数的单调性求出函数的最值,得到数列的最小项.
方法二:通过bn+1-bn比较大小,判断函数的单调性,讨论a的值,通过函数的单调性求出函数的最值,得到数列的最小项.
(Ⅱ)方法一:通过
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
方法二:通过bn+1-bn比较大小,判断函数的单调性,讨论a的值,通过函数的单调性求出函数的最值,得到数列的最小项.
解答:
解:(Ⅰ) 由a2,S2,a3成等差,有2S2=a2+a3,2(a1+a2)=a2+a3,
a3=2a1+a2,a1q2=2a1+a1q,q2-q-2=0,q=-1,q=2,
由an>0,q=2.
故an=2n.
(Ⅱ)方法一:bn=(1-
)2+a(1+
),
令
=t∈{
,
,
,…,
,…},
则bn=(1-2t)2+a(1+t)=4t2+(a-4)t+a+1,
对称轴t=
=
,
①当0≤a<1时,对称轴t=
>
,数列{bn}单调递增,最小项为b1=
a;
②当a=1时,对称轴t=
=
,恰好位于
与
的中间,则b1=b2,
故n>1时,数列{bn}单调递增,最小项为b1=b2=
;
③当1<a≤2时,对称轴t=
∈[
,
),位于
与
之间而靠近于
,
故n>1时,数列{bn}单调递增,b1>b2,最小项为b2=
a+
.
方法二:由bn=(1-
)2+a(1+
)=(1-
)2+a(1+
),
则bn+1=(1-
)2+a(1+
),
bn+1-bn=(1-
)2+a(1+
)-(1-
)2-a(1+
)
=(2-
-
)(
-
)+a(
-
)=(
-
)(a-4+
+
),
由
-
<0,
①当a-4+
+
<0,得a<4-
-
,
函数f(n)=4-
-
单调递增,即a<f(1)=1,bn+1-bn>0,数列{bn}单调递增,
最小项为b1=
a;
②当a=1时,b2-b1=0,n>1,a-4+
+
=
+
-3<0,bn+1-bn>0,
故n>1时,数列{bn}单调递增,最小项为b1=b2=
;
③由b3-b2=(
-
)(a-4+
+
)=0,求得a=
,则当1<a≤2<
时,b1=
a,b2=
a+
,b1-b2=
a-
>0,b1>b2,n>1,a-4+
+
≤
+
-2<0,
得bn+1-bn>0,
故n>1时,数列{bn}单调递增,最小项为b2=
a+
.
a3=2a1+a2,a1q2=2a1+a1q,q2-q-2=0,q=-1,q=2,
由an>0,q=2.
故an=2n.
(Ⅱ)方法一:bn=(1-
| 2 |
| 2n |
| 1 |
| 2n |
令
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
则bn=(1-2t)2+a(1+t)=4t2+(a-4)t+a+1,
对称轴t=
| a-4 |
| -8 |
| 4-a |
| 8 |
①当0≤a<1时,对称轴t=
| 4-a |
| 8 |
| 3 |
| 8 |
| 3 |
| 2 |
②当a=1时,对称轴t=
| 4-a |
| 8 |
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
故n>1时,数列{bn}单调递增,最小项为b1=b2=
| 3 |
| 2 |
③当1<a≤2时,对称轴t=
| 4-a |
| 8 |
| 1 |
| 4 |
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
故n>1时,数列{bn}单调递增,b1>b2,最小项为b2=
| 5 |
| 4 |
| 1 |
| 4 |
方法二:由bn=(1-
| 2 |
| an |
| 1 |
| an |
| 2 |
| 2n |
| 1 |
| 2n |
则bn+1=(1-
| 2 |
| 2n+1 |
| 1 |
| 2n+1 |
bn+1-bn=(1-
| 2 |
| 2n+1 |
| 1 |
| 2n+1 |
| 2 |
| 2n |
| 1 |
| 2n |
=(2-
| 2 |
| 2n+1 |
| 2 |
| 2n |
| 2 |
| 2n |
| 2 |
| 2n+1 |
| 1 |
| 2n+1 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n |
| 4 |
| 2n+1 |
| 4 |
| 2n |
由
| 1 |
| 2n+1 |
| 1 |
| 2n |
①当a-4+
| 4 |
| 2n+1 |
| 4 |
| 2n |
| 4 |
| 2n+1 |
| 4 |
| 2n |
函数f(n)=4-
| 4 |
| 2n+1 |
| 4 |
| 2n |
最小项为b1=
| 3 |
| 2 |
②当a=1时,b2-b1=0,n>1,a-4+
| 4 |
| 2n+1 |
| 4 |
| 2n |
| 4 |
| 2n+1 |
| 4 |
| 2n |
故n>1时,数列{bn}单调递增,最小项为b1=b2=
| 3 |
| 2 |
③由b3-b2=(
| 1 |
| 23 |
| 1 |
| 22 |
| 4 |
| 23 |
| 4 |
| 22 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 4 |
| 2n+1 |
| 4 |
| 2n |
| 4 |
| 2n+1 |
| 4 |
| 2n |
得bn+1-bn>0,
故n>1时,数列{bn}单调递增,最小项为b2=
| 5 |
| 4 |
| 1 |
| 4 |
点评:本题考查数列的通项公式的求法,老师的函数特征,数列与不等式相结合,求解数列的最小值,考查分析问题解决问题的能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
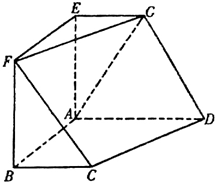 如图,在六面体ABCDEFG中,平面EFG∥平面ABCD,AE⊥平面ABCD,EF⊥AE,AE=AB=AD,EG=BC,且EF=2EG.
如图,在六面体ABCDEFG中,平面EFG∥平面ABCD,AE⊥平面ABCD,EF⊥AE,AE=AB=AD,EG=BC,且EF=2EG. 已知圆A的方程为(x+1)2+y2=16,点B的坐标为(1,0),P是圆A上任意一点,线段BP的垂直平分线与AP交于点C.
已知圆A的方程为(x+1)2+y2=16,点B的坐标为(1,0),P是圆A上任意一点,线段BP的垂直平分线与AP交于点C.
 如图是某班第1和第2小组学生身高的茎叶图(单位:cm),则这两个小组学生身高中位数的等差中项为
如图是某班第1和第2小组学生身高的茎叶图(单位:cm),则这两个小组学生身高中位数的等差中项为