题目内容
3.不等式(2-a)x2-2(a-2)+4>0对于一切实数都成立,则( )| A. | {a|-2<a≤2} | B. | {a|-2<a<2} | C. | {a|a<-2} | D. | {a|a<-2或a>2} |
分析 分类讨论:当a=2时;当a≠0时,由题意可得$\left\{\begin{array}{l}{2-a>0}\\{△<0}\end{array}\right.$,解出即可.
解答 解:①当a=2时,原不等式化为4>0,因此a=2适合;
②当a≠0时,由题意可得$\left\{\begin{array}{l}{2-a>0}\\{△=4(a-2)^{2}-16(2-a)<0}\end{array}\right.$,
化为$\left\{\begin{array}{l}{a<2}\\{(a-2)(a+2)<0}\end{array}\right.$,解得-2<a<2.
综上可知:a的取值范围为{a|-2<a≤2}.
故选:A.
点评 本题考查了函数恒成立,二次函数的性质,一元二次不等式的解法、分类讨论等基础知识与基本技能方法,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
13.已知x>0,y>0,且x+y=2xy,则x+4y的最小值为( )
| A. | 4 | B. | $\frac{7}{2}$ | C. | $\frac{9}{2}$ | D. | 5 |
18.若集合A={x|(k+2)x2+2kx+1=0}有且仅有1个元素,则实数k的值是( )
| A. | ±2或-1 | B. | -2或-1 | C. | 2或-1 | D. | -2 |
12.若$\overrightarrow a=(2cosα,1)$,$\overrightarrow b=(sinα,1)$,且$\overrightarrow a∥\overrightarrow b$,则tanα=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{1}{2}$ |
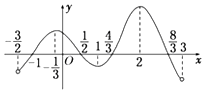 已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].
已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].