题目内容
17.已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为( )| A. | $\stackrel{∧}{y}$=1.23x+5 | B. | $\stackrel{∧}{y}$=1.23x+4 | C. | $\stackrel{∧}{y}$=0.08x+1.23 | D. | $\stackrel{∧}{y}$=1.23x+0.08 |
分析 根据线性回归直线方程一定过样本中心点,选择验证法或排除法即可,具体方法就是将点(4,5)的坐标分别代入各个选项,满足的即为所求.
解答 解:【解法一】由回归直线的斜率的估计值为1.23,可排除C,
由线性回归直线方程样本点的中心为(4,5),
将x=4分别代入A、B、C,其值依次为8.92、9.92、5,排除A、B.
【解法二】因为回归直线方程一定过样本中心点,
将样本点的中心(4,5)分别代入各个选项,只有D满足.
故选:D.
点评 本题考查了线性回归直线方程的应用问题,是基础题目.

练习册系列答案
相关题目
12.若$\overrightarrow a=(2cosα,1)$,$\overrightarrow b=(sinα,1)$,且$\overrightarrow a∥\overrightarrow b$,则tanα=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{1}{2}$ |
2.若函数f(x)=lg(x2+ax-a-1)在区间(2,+∞)上单调递增,则实数a的取值范围是( )
| A. | (-3,+∞) | B. | [-3,+∞) | C. | (-4,+∞) | D. | [-4,+∞) |
9.已知函数f(x)=cos(cosx),下列结论错误的是( )
| A. | f(x)是奇函数 | B. | π为f(x)的最小正周期 | ||
| C. | f(x)的对称轴方程为x=kπ(k∈Z) | D. | f(x)的值域为[cos1,1] |
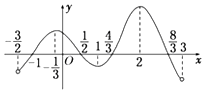 已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].
已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].