题目内容
15.已知定义在R上函数y=f(x+1)是偶函数,且在[1,+∞)上单调,若数列{an}是公差不为0的等差数列,且f(a6)=f(a20),则{an}的前25项之和为( )| A. | 0 | B. | $\frac{25}{2}$ | C. | 25 | D. | 50 |
分析 由已知得函数y=f(x)对任意自变量x都有f(x+1)=f(1-x),即有函数f(x)图象关于直线x=1对称,从而得到a6+a20=2,运用等差数列的求和公式,由此能求出结果.
解答 解:由定义在R上函数y=f(x+1)是偶函数,
可得函数y=f(x)对任意自变量x都有f(x+1)=f(1-x),
∴函数f(x)图象关于直线x=1对称,
又函数f(x)在[1,+∞)上单调,
数列{an}是公差不为0的等差数列,且f(a6)=f(a20),
∴a6+a20=2,
∴S25=$\frac{25}{2}$(a1+a25)=$\frac{25}{2}$(a6+a20)=$\frac{25}{2}$×2=25.
故选:C.
点评 本题考查等差数列的前25项之和的求法,是中档题,注意函数性质和等差数列的性质的合理运用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的外接球的表面积是( )
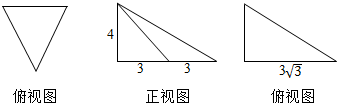

| A. | 208π | B. | 128π | C. | 64π | D. | 32π |
3.若实数x,y满足$\left\{\begin{array}{l}{x-2y≤0}\\{2x-y≥0}\\{x+y≥3}\end{array}\right.$,则下列不等成立的是( )
| A. | x2+y2≥5 | B. | $\frac{y}{x-2}$≥-2 | C. | 2x+y≥5 | D. | |x+3y-1|≥4 |
1.不等式$\frac{5-x}{x-1}≥1$的解集为( )
| A. | (-∞,-3)∪(3,+∞) | B. | (-∞,1)∪(3,+∞) | C. | [1,3] | D. | (1,3] |