题目内容
3.若实数x,y满足$\left\{\begin{array}{l}{x-2y≤0}\\{2x-y≥0}\\{x+y≥3}\end{array}\right.$,则下列不等成立的是( )| A. | x2+y2≥5 | B. | $\frac{y}{x-2}$≥-2 | C. | 2x+y≥5 | D. | |x+3y-1|≥4 |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,距离,斜率以及截距进行求解对应的范围即可得到结论.
解答 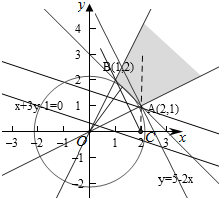 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
A.设z=x2+y2,则z的几何意义为区域内的点到原点的距离的平方,
由图象知点O到直线x+y=3的距离最小,此时d=$\frac{|3|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$<5,
则A.x2+y2≥5不成立,
B.$\frac{y}{x-2}$的几何意义为区域内的点到点C(2,0)的斜率,
由图象知BC的斜率最小,此时k=$\frac{2}{1-2}$=-2,
则$\frac{y}{x-2}$≥-2成立,
但当x=2,y=1时,$\frac{y}{x-2}$无意义,则$\frac{y}{x-2}$≥-2不一定成立,
C.当x=1,y=2时,2x+y=2+2=4≥5不成立,
D.|x+3y-1|=$\sqrt{10}$•$\frac{|x+3y-1|}{\sqrt{10}}$,
设d=$\frac{|x+3y-1|}{\sqrt{10}}$,则|x+3y-1|=$\sqrt{10}$•d,
则d的几何意义是区域内的点到直线x+3y-1=0的距离,
由图象知A(2,1)到直线x+3y-1=0的距离最小,
此时d=$\frac{|2+3-1|}{\sqrt{10}}$=$\frac{4}{\sqrt{10}}$,
则|x+3y-1|=$\sqrt{10}$•d=$\sqrt{10}$•$\frac{4}{\sqrt{10}}$=4,
即|x+3y-1|≥4成立.
故选:D.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,将不等式转化为距离,斜率以及截距进行求解是解决本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.已知定义在R上函数y=f(x+1)是偶函数,且在[1,+∞)上单调,若数列{an}是公差不为0的等差数列,且f(a6)=f(a20),则{an}的前25项之和为( )
| A. | 0 | B. | $\frac{25}{2}$ | C. | 25 | D. | 50 |
8.点O为△ABC内一点,且满足$\overrightarrow{OA}+\overrightarrow{OB}+4\overrightarrow{OC}=\overrightarrow{0}$,设△OBC与△ABC的面积分别为S1、S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |