题目内容

5．某几何体的三视图如图所示，则该几何体的外接球的表面积是（　　）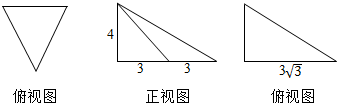
A．208πB．128πC．64πD．32π

分析 几何体为三棱锥，且三棱锥的一条侧棱垂直于底面，结合直观图判断外接球半径，代入求得表面积公式计算．

解答 解：由三视图知：几何体为三棱锥，且三棱锥的一条侧棱垂直于底面，高为4，
底面为等腰三角形，底边长为6，高为3$\sqrt{3}$．
∴△ABC为等边三角形，外接圆的半径r=2$\sqrt{3}$，
∴几何体的外接球的半径R=$\frac{1}{2}$$\sqrt{16+48}$=4，
∴外接球的表面积S=4π×16=64π．
故选：C．

点评 本题考查了由三视图求几何体的外接球的表面积，根据三视图判断几何体的结构特征，利用几何体的结构特征与数据求得外接球的半径是解答本题的关键．

练习册系列答案
相关题目
15．命题p：|x-m|＜1成立的一个充分条件是q：1＜x＜2，则实数m的取值范围是[1，2]．
16．如图，已知四边形ABCD是矩形，PA⊥平面ABC，M，N分别是AB，PC的中点．
（1）求证：MN⊥AB；
（2）若PA=AD，求证：MN⊥平面PCD．
13．若2，3，x组成一个锐角三角形的三边，求x的取值范围．
20．某企业的4名职工参加职业技能考核，每名职工均可从4个备选考核项项目中任意抽取一个参加考核，则恰有一个项目未被抽中的概率为（　　）
A．$\frac{9}{16}$B．$\frac{27}{64}$C．$\frac{81}{256}$D．$\frac{7}{16}$
10．已知{$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$}是空间的一个基底，{$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{a}$-$\overrightarrow{b}$，$\overrightarrow{c}$}是空间的另一个基底，一向量$\overrightarrow{p}$在基底{$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$}下的坐标为（4，2，3），则向量$\overrightarrow{p}$在基底{$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{a}$-$\overrightarrow{b}$，$\overrightarrow{c}$}下的坐标是（　　）
A．（4，0，3）B．（3，1，3）C．（1，2，3）D．（2，1，3）
17．函数y=$\frac{1}{\sqrt{{x}^{2}+px+q}}$的定义域为（-∞，-1）∪（2，+∞），则p=-1，q=-2．
14．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$-2$\overrightarrow{b}$|=1，|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2，则$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{8}$．
15．已知定义在R上函数y=f（x+1）是偶函数，且在[1，+∞）上单调，若数列{an}是公差不为0的等差数列，且f（a6）=f（a20），则{an}的前25项之和为（　　）
A．0B．$\frac{25}{2}$C．25D．50

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网