题目内容
17.若a>0,b>0,且函数f(x)=4x3-ax2-bx+2在x=1处有极值,则ab的最大值等于( )| A. | 4 | B. | 8 | C. | 9 | D. | 18 |
分析 求出导函数,利用函数在极值点处的导数值为0得到a,b满足的条件,利用基本不等式求出ab的最值.
解答 解:由题意,求导函数f′(x)=12x2-2ax-2b,
∵在x=1处有极值,
∴a+b=6,
∵a>0,b>0
∴ab≤$(\frac{a+b}{2})^{2}$=9,当且仅当a=b=3时取等号,
所以ab的最大值等于9,
故选:C.
点评 本题考查函数在极值点处的导数值为0、考查利用基本不等式求最值,需注意:一正、二定、三相等.

练习册系列答案
相关题目
12.设等比数列{an}的前n项和为Sn,若$\frac{{S}_{6}}{{S}_{3}}$=3,则$\frac{{a}_{11}}{{a}_{2}}$( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
9.“$\frac{1}{a}$>$\frac{1}{b}$”是“a<b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |

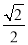 B.
B.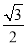
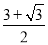 D.
D.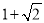
 的值域是__________.
的值域是__________.