题目内容
2.若直线l1的一个法向量$\overrightarrow{n}$=(1,1),若直线l2的一个方向向量$\overrightarrow{d}$=(1,-2),则l1与l2的夹角θ=arccos$\frac{\sqrt{10}}{10}$.(用反三角函数表示)分析 利用向量的夹角公式,即可得出结论.
解答 解:由题意,cosθ=|$\frac{1-2}{\sqrt{2}•\sqrt{5}}$|=$\frac{\sqrt{10}}{10}$,
∴θ=arccos$\frac{\sqrt{10}}{10}$.
故答案为:arccos$\frac{\sqrt{10}}{10}$.
点评 本题考查向量的夹角公式,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
10.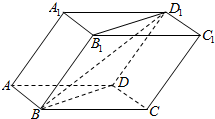 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )
 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{\sqrt{39}}{3}$ |
11.若在△ABC中,∠A=30°,b=3,S△ABC=$\sqrt{3}$,则$\frac{a+b+c}{sinA+sinB+sinC}$=( )
| A. | $\sqrt{13}$ | B. | $\frac{{\sqrt{21}}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $13\sqrt{2}$ |
 表示复数
表示复数 的共轭复数,则
的共轭复数,则 ( )
( ) B.5 C.
B.5 C. D.6
D.6 ,则要得到其导函数
,则要得到其导函数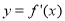 的图象,只需将函数
的图象,只需将函数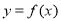 的图象( )
的图象( )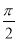 个单位
个单位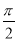 个单位
个单位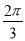 个单位
个单位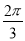 个单位
个单位