题目内容
定积分
cos2xdx等于（ ）
| ∫ |
-
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：定积分
专题：导数的概念及应用
分析：根据积分公式，即可得到结论．
解答：
解：
cos2xdx=
dx=（
x+
sin2x）
=
．
故选：D．
| ∫ |
-
|
| ∫ |
-
|
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| | |
-
|
| π |
| 2 |
故选：D．
点评：本题主要考查了定积分的计算．解题的关键是要能求出被积函数的一个原函数然后再根据牛顿-莱布尼茨公式求解
练习册系列答案
口算能手系列答案
相关题目
若两直线3x+2y+m=0和x-4y+n=0的交点坐标为（-1，2），则m+n等于（ ）
| A、8 | B、10 | C、-8 | D、-10 |
如图是某几何体的三视图，则该几何体的表面积为（ ）
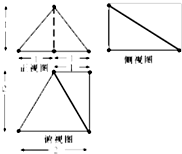
A、
| ||||||||
B、
| ||||||||
C、4+
| ||||||||
D、
|
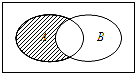已知全集U=R，集合A={0，1，2}，B={2，3，4}，如图阴影部分所表示的集合为（ ）| A、{2} |
| B、{0，1} |
| C、{3，4} |
| D、{0，1，2，3，4} |
已知O为锐角△ABC的外心，AB=6，AC=4，若
=x
+y
，且x+4y=2，则cos∠BAC=（ ）
| AO |
| AB |
| AC |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
下列命题中，错误的是（ ）
| A、若a＞b，c＜d，则a-c＞b-d | ||||||
| B、若a＞b＞0，c＜d＜0，则ac＜bd | ||||||
C、若a＞b，则
| ||||||
D、若a＞b，则
|
复数-1+i在复平面内表示的点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |